题目内容
【题目】如图，E是正方形ABCD对角线BD上一点，EM⊥BC，EN⊥CD垂足分别是求M、N
（1）求证：AE=MN；
（2）若AE=2，∠DAE=30°，求正方形的边长．
【答案】
（1）
证明：连接EC．
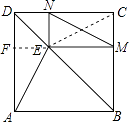
∵四边形ABCD是正方形，EM⊥BC，EN⊥CD，
∴∠NCM=∠CME=∠CNE=90°，
∴四边形EMCN为矩形．
∴MN=CE．
又∵BD为正方形ABCD的对角线，
∴∠ABE=∠CBE．
在△ABE和△CBE中
∵ 
，
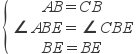∴△ABE≌△CBE（SAS）．
∴AE=EC．
∴AE=MN．
（2）
解：过点E作EF⊥AD于点F，
∵AE=2，∠DAE=30°，
∴EF= 
AE=1，AF=AEcos30°=2× 
= 
．
∵BD是正方形ABCD的对角线，
∴∠EDF=45°，
∴DF=EF=1，
∴AD=AF+DF= +1，即正方形的边长为 +1．
【解析】（1）连接EC，根据题意可得出四边形EMCN为矩形，故MN=CE，再由SAS定理得出△ABE≌△CBE，进而可得出结论；（2）过点E作EF⊥AD，由直角三角形的性质可得出EF及AF的长，再由等腰直角三角形的性质得出DF的长，进而可得出结论．
【考点精析】利用正方形的性质对题目进行判断即可得到答案，需要熟知正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
