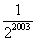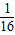题目内容
已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2003个三角形的周长为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据三角形的中位线定理,第一个三角形的周长为1,推导出第二个三角形的周长
,第三个三角形的周长为
,然后由前几个三角形的周长,寻找周长之间的规律.
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:由于三角形的中位线平行于第三边并且等于它的一半,三条中位线组成的三角形的周长是原三角形的周长的一半,以此类推,第2003个三角形的周长为(
×
×
×…×
)[2002个]=
.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22002 |
故选C.
点评:本题考查了三角形中位线的性质,比较简单,但在解答时要查找规律.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
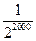
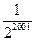
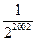
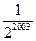
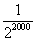 B、
B、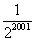 C、
C、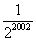 D、
D、