题目内容
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.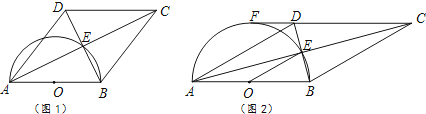
(1)利用图1,求证:四边形ABCD是菱形.
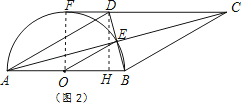
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
【答案】
(1)
证明:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)
证明:①连结OF.
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,
∴OF即为△ABD中AB边上的高.
∴S△ABD= ![]() AB×OF=
AB×OF= ![]() ×8×4=16,
×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE= ![]() S△ABD=4.
S△ABD=4.
②过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
∵在Rt△DAH中,sin∠DAB= ![]() =
= ![]() ,
,
∴∠DAH=30°.
∵点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°.
∴∠AOE=180°﹣∠EOB=150°.
∴弧AE的长= ![]() =
= ![]() .
.
【解析】(1)先由AE=EC、BE=ED可判定四边形为平行四边形,再根据∠AEB=90°可判定该平行四边形为菱形;(2)①连结OF,由切线可得OF为△ABD的高且OF=4,从而可得S△ABD , 由OE为△ABD的中位线可得S△OBE= ![]() S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB=
S△ABD; ②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB= ![]() =
= ![]() 知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.
知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.

 名校课堂系列答案
名校课堂系列答案【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 | 7:30 | 11:15 | 2:50 |
首尔时间 | 8:30 | 12:15 | 3:50 |
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?