题目内容
 如图,矩形内两相邻正方形的面积分别为2和6,请计算大矩形内阴影部分的面积.
如图,矩形内两相邻正方形的面积分别为2和6,请计算大矩形内阴影部分的面积.分析:根据正方形的面积公式求得两个正方形的边长分别是
,
,再根据阴影部分的面积等于矩形的面积减去两个正方形的面积进行计算.
| 2 |
| 6 |
解答:解:∵矩形内两相邻正方形的面积分别为2和6,
∴两个正方形的边长分别为:
,
,
∴大矩形内阴影部分的面积为:大矩形面积-2-6=(
+
)×
-8=2
-2.
∴两个正方形的边长分别为:
| 2 |
| 6 |
∴大矩形内阴影部分的面积为:大矩形面积-2-6=(
| 2 |
| 6 |
| 6 |
| 3 |
点评:此题主要考查了二次根式的应用,能够由正方形的面积表示出正方形的边长,再进一步表示矩形的长是解题关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,矩形内两相邻正方形的面积分别是2和6,那么矩形内阴影部分的面积是( )
如图,矩形内两相邻正方形的面积分别是2和6,那么矩形内阴影部分的面积是( )A、2
| ||
B、3
| ||
C、2
| ||
D、6-2
|
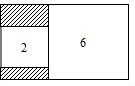 如图,矩形内两相邻正方形的面积分别是2和6,那么矩形内阴影部分的面积是
如图,矩形内两相邻正方形的面积分别是2和6,那么矩形内阴影部分的面积是 如图,矩形内两相邻正方形的面积分别是2和6,有以下四个结论:
如图,矩形内两相邻正方形的面积分别是2和6,有以下四个结论:
 ;②小正方形的边长为
;②小正方形的边长为 ;③矩形内阴影部分的面积为2
;③矩形内阴影部分的面积为2 -2;④大矩形的面积为6+3
-2;④大矩形的面积为6+3