题目内容
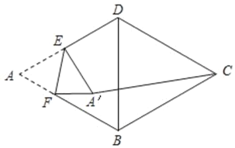
【题目】如图,BD是菱形ABCD的对角线,E是边AD的中点,F是边AB上的一点,将△AEF沿EF所在的直线翻折得到△A′EF,连结A′C.若AB=5,BD=6,当点A′到∠A的两边的距离相等时,A′C的长是_____.
【答案】4
【解析】
由菱形的性质可得AB=BC=CD=AD=5,BD⊥AC,DO=BO=![]() BD=3,AO=CO,AC平分∠DAB,由勾股定理可求AO,AC的长,由角平分线的性质可得点A'在线段AC上,由平行线分线段成比例可求AH的长,即可求A'C的长.
BD=3,AO=CO,AC平分∠DAB,由勾股定理可求AO,AC的长,由角平分线的性质可得点A'在线段AC上,由平行线分线段成比例可求AH的长,即可求A'C的长.
如图,连接AC,
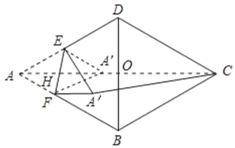
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,BD⊥AC,DO=BO=![]() BD=3,AO=CO,AC平分∠DAB,
BD=3,AO=CO,AC平分∠DAB,
∴AO=![]() =4,
=4,
∴AC=2AO=8,
∵点A′到∠DAB的两边的距离相等,
∴点A'在∠DAB的平分线上,即点A'在线段AC上,
∵将△AEF沿EF所在的直线翻折得到△A′EF,
∴AH=A'H,EF⊥AC,
∴EF∥DB,
∴![]() ,
,
∴AO=2AH,
∴AH=2,
∴A'C=AC﹣AA'=8﹣4=4,
故答案为:4

练习册系列答案
相关题目