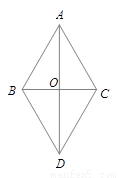题目内容
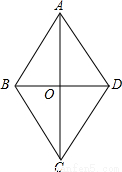
在菱形ABCD中，对角线AC、BD相交于O，AB=5，BD=8，则菱形ABCD的面积=
- A.24
- B.40
- C.48
- D.20
A
分析：根据菱形性质得出AC⊥BD，OD=OB=
BD=4，AC=2OA=2OC，在Rt△AOB中，由勾股定理求出OA，代入AC×BD求出即可．
解答：
∵四边形ABCD是菱形，
∴AC⊥BD，OD=OB=BD=4，AC=2OA=2OC，
在Rt△AOB中，由勾股定理得：AO=
=
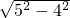=3，
∴AC=2OA=6，
∴菱形ABCD的面积是AC×BD=×6×8=24，
故选A．
点评：本题考查了菱形的性质和勾股定理注意：菱形的对角线平分且垂直，菱形ABCD的面积=AC×BD．
分析：根据菱形性质得出AC⊥BD，OD=OB=
BD=4，AC=2OA=2OC，在Rt△AOB中，由勾股定理求出OA，代入AC×BD求出即可．解答：
∵四边形ABCD是菱形，
∴AC⊥BD，OD=OB=
BD=4，AC=2OA=2OC，在Rt△AOB中，由勾股定理得：AO=
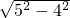==3，∴AC=2OA=6，
∴菱形ABCD的面积是
AC×BD=×6×8=24，故选A．
点评：本题考查了菱形的性质和勾股定理注意：菱形的对角线平分且垂直，菱形ABCD的面积=
AC×BD． 
练习册系列答案
阅读快车系列答案
相关题目
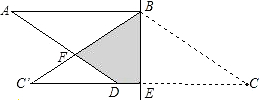如图，在菱形ABCD中，BE⊥CD于点E，AB=5，BE=3，把菱形沿着BE对折，使点C落在点C′处，则重叠部分（即阴影部分）的面积是
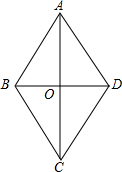（2012•玉林）如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC≠BD，则图中全等三角形有（ ）
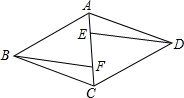（2012•百色）如图，在菱形ABCD中，E、F是对角线AC上的两点，且AE=CF．
