题目内容
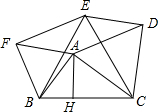 如图所示,以△ABC的三边为边在BC的同侧作正三角形BCE,正三角形ABF和正三角形ACD,已知BC=3,高AH=1,则五边形BCDEF的面积是
如图所示,以△ABC的三边为边在BC的同侧作正三角形BCE,正三角形ABF和正三角形ACD,已知BC=3,高AH=1,则五边形BCDEF的面积是分析:由正△ABF、正△BCE、正△ACD和正△BCE可知:△ABC≌△FBE≌△DEC,所以S△ABC=S△FBE=S△DEC=
×3×1=
,又因为S△BCE=
×3×3×sin60°=
×
,所以五边形BCDEF的面积=S△BCE+S△FBE+S△DEC.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
解答:解:∵正三角形ABF和正△BCE
∴AB=BF BC=BE∠ABC=∠FBE=60°-∠EBA
∴△ABC≌△FBE
同理∵正三角形ACD和BCE
∴AC=DC BC=EC∠ACB=∠DCE=60°-∠ECA
∴△ABC≌△DEC
∴△ABC≌△FBE≌△DEC
∴S△ABC=S△FBE=S△DEC=
×3×1=
又∵S△BCE=
×3×3×sin60°=
×
∴五边形BCDEF的面积=S△BCE+S△FBE+S△DEC=
×
+
+
=3+
∴AB=BF BC=BE∠ABC=∠FBE=60°-∠EBA
∴△ABC≌△FBE
同理∵正三角形ACD和BCE
∴AC=DC BC=EC∠ACB=∠DCE=60°-∠ECA
∴△ABC≌△DEC
∴△ABC≌△FBE≌△DEC
∴S△ABC=S△FBE=S△DEC=
| 1 |
| 2 |
| 3 |
| 2 |
又∵S△BCE=
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
∴五边形BCDEF的面积=S△BCE+S△FBE+S△DEC=
| 9 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
9
| ||
| 4 |
点评:解决本题的关键是根据所给条件得到所求的五边形的组成的相应的三角形全等.

练习册系列答案
相关题目
 30、如图所示,以△ABC的三边为边,分别作三个等边三角形.
30、如图所示,以△ABC的三边为边,分别作三个等边三角形.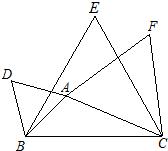 29、如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.
29、如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.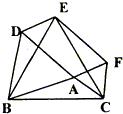 24、已知:如图所示,以△ABC的三边为边,在BC的同侧分别作等边△ABD、△BCE、△ACF.
24、已知:如图所示,以△ABC的三边为边,在BC的同侧分别作等边△ABD、△BCE、△ACF.