Question

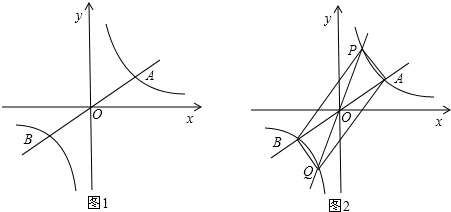
如图1，已知双曲线y=

k

x

(k＞0)与直线y=k₁x交于A，B两点，点A在第一象限．试解答下列问题：
（1）若点A的坐标为（4，2），则点B的坐标为

 

；
（2）若点A的横坐标为m，则点B的坐标可表示为

 

；（用m、k表示）
（3）如图2，过原点O作另一条直线y=k₂x（k₁≠k₂），交双曲线y=

k

x

(k＞0)于P，Q两点，点P在第一象限，求证：四边形APBQ一定是平行四边形；
（4）如图3，当k=12，k₁=

3

4

，k2=

4

3

时，判定四边形APBQ的形状，并证明．

Answer 1

分析：（1）根据A点的坐标求出直线和双曲线的函数表达式，然后即可推出B点的坐标；
（2）首先把A点的横坐标代入到双曲线，求出A点的横坐标，根据（1）的结论分析，A、B两边的横纵坐标互为相反数，即可推出B点的坐标；
（3）首先设出A的坐标，然后推出B点的坐标，根据勾股定理，即可推出OA、OB的长度，同理即可推出OP=OQ，即可推出四边形APBQ是平行四边形；
（4）根据题意，推出直线AB、直线PQ、双曲线的函数表达式，即可推出A、B、P、Q的坐标，然后根据勾股定理推出OA=OB=5，OP=OQ=5，推出AB=PQ=10，即可推出四边形APBQ是矩形．

解答：解：（1）∵双曲线y=

k

x

(k＞0)与直线y=k₁x相交于A、B两点，且A（4，2），
∴k=8，k₁=

1

2

，
∴y=

8

x

，y=

1

2

x，
∴B点的坐标为（-4，-2）；

（2）∵点A的横坐标为m，双曲线y=

k

x

(k＞0)过A点，
∴A（m，

k

m

），
∴B（-m，-

k

m

）；

（3）设A的坐标（m，

k

m

），则B点的坐标（-m，-

k

m

）
由勾股定理OA=

m2+(k′m)2

，
OB=

(-m)2+( -k m )2

=

m2+( k m )2

，
∴OA=OB（6分）
同理可得OP=OQ，（7分）
∴四边形APBQ是平行四边形；
（4）四边形APBQ是矩形，理由：

y= 12 x y= 3 4 x

，解得

x=4 y=3

或

x=-4 y=-3

，
∵点A在第一象限，
∴A（4，3），B（-4，-3）

y= 12 x y= 4 3 x

，解得

x=3 y=4

或

x=-3 y=-4

，
∵点P在第一象限，∴P（3，4），Q（-3，-4）
由勾股定理OA=OB=

32+42

=5，OP=OQ=

42+32

=5，
∴四边形APBQ是平行四边形，
∵AB=PQ=10
∴四边形APBQ是矩形．（12分）

点评：本题主要考查根据双曲线与直线相交求交点的坐标，平行四边形的判定，矩形的判定，勾股定理，关键在于根据题意求出各交点的坐标．