题目内容
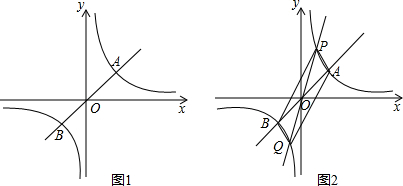
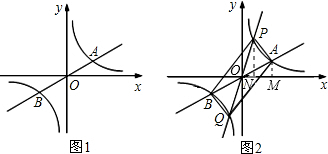
如图1,已知双曲线y1=
(k>0)与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为
(2)当x满足:
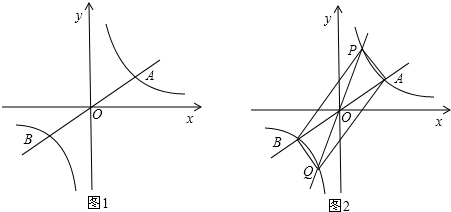
(3)过原点O作另一条直线l,交双曲线y=
(k>0)于P,Q两点,点P在第一象限,如图2所示.
①四边形APBQ一定是
②若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
| k |
| x |
(1)若点A的坐标为(3,1),则点B的坐标为
(-3,-1)
(-3,-1)
;(2)当x满足:
-3≤x<0或x≥3
-3≤x<0或x≥3
时,y1≤y2;(3)过原点O作另一条直线l,交双曲线y=
| k |
| x |
①四边形APBQ一定是
平行四边形
平行四边形
;②若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.

分析:(1)由A和B为正比例函数与反比例函数的交点,得到A和B关于原点对称,由A的坐标即可求出B的坐标;
(2)由A和B的横坐标及原点的横坐标0,将x轴分为四个范围,分别为:x<-3,-3<x<0,0<x<3,x>3,找出一次函数在反比例函数上方的范围即可;
(3)①由OP=OQ,OA=OB,利用对角线互相平分的四边形为平行四边形可得四边形APBQ一定是平行四边形;
②由A得坐标确定出反比例函数解析式,将P得横坐标x=1代入反比例解析式中,求出P的纵坐标,确定出P的坐标,过P作PN垂直于x轴,过A作AM垂直于x轴,可得出PN,AM,ON,OM的长,进而求出MN的长,根据四边形OPAM的面积-三角形AOM的面积表示出三角形AOP的面积,而四边形OPAM的面积=三角形OPN的面积+梯形AMNP的面积,可求出三角形AOP的面积,在三角形ABP中,由O为AB的中点,根据等底同高得到三角形AOP的面积与三角形BOP的面积相等,同理得到三角形BOQ的面积=三角形AOQ的面积=三角形AOP的面积=三角形BOP的面积,而这四个三角形的面积之和为平行四边形APBQ的面积,即可求出四边形APBQ的面积.
(2)由A和B的横坐标及原点的横坐标0,将x轴分为四个范围,分别为:x<-3,-3<x<0,0<x<3,x>3,找出一次函数在反比例函数上方的范围即可;
(3)①由OP=OQ,OA=OB,利用对角线互相平分的四边形为平行四边形可得四边形APBQ一定是平行四边形;
②由A得坐标确定出反比例函数解析式,将P得横坐标x=1代入反比例解析式中,求出P的纵坐标,确定出P的坐标,过P作PN垂直于x轴,过A作AM垂直于x轴,可得出PN,AM,ON,OM的长,进而求出MN的长,根据四边形OPAM的面积-三角形AOM的面积表示出三角形AOP的面积,而四边形OPAM的面积=三角形OPN的面积+梯形AMNP的面积,可求出三角形AOP的面积,在三角形ABP中,由O为AB的中点,根据等底同高得到三角形AOP的面积与三角形BOP的面积相等,同理得到三角形BOQ的面积=三角形AOQ的面积=三角形AOP的面积=三角形BOP的面积,而这四个三角形的面积之和为平行四边形APBQ的面积,即可求出四边形APBQ的面积.
解答:解:(1)由A和B为反比例函数与一次函数的交点,
得到A和B关于原点对称,
∵A(3,1),
∴B(-3,-1);
(2)由图象可得:当-3≤x<0或x≥3时,y1≤y2;
(3)①∵OP=OQ,OA=OB,
∴四边形APBQ为平行四边形;
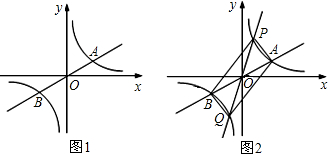
②过A作AM⊥x轴,过P作PN⊥x轴,如图所示:
由A(3,1)在反比例函数图象上,得到反比例解析式为y=
,
∵P的横坐标为1,P在反比例函数图象上,
∴将x=1代入反比例解析式得:y=3,即P(1,3),
∴AM=1,OM=3,PN=3,ON=1,MN=OM-ON=2,
则S△AOP=S四边形OPAM-S△AOM=S△PON+S梯形AMNP-S△AOM
=
PN•ON+
(AM+PN)•MN-
AM•OM
=
×3×1+
×(1+3)×2-
×1×3
=4,
在△APB中,O为AB的中点,即AO=BO,
∴S△AOP=S△BOP,
同理S△BOQ=S△AOQ=S△AOP=S△BOP,
又∵S平行四边形APBQ=S△BOQ+S△AOQ+S△AOP+S△BOP,
∴S平行四边形APBQ=4S△AOP=16.
故答案为:(1)(-3,-1);(2)-3≤x<0或x≥3;(3)①平行四边形
得到A和B关于原点对称,
∵A(3,1),
∴B(-3,-1);
(2)由图象可得:当-3≤x<0或x≥3时,y1≤y2;
(3)①∵OP=OQ,OA=OB,
∴四边形APBQ为平行四边形;
②过A作AM⊥x轴,过P作PN⊥x轴,如图所示:

由A(3,1)在反比例函数图象上,得到反比例解析式为y=
| 3 |
| x |
∵P的横坐标为1,P在反比例函数图象上,
∴将x=1代入反比例解析式得:y=3,即P(1,3),
∴AM=1,OM=3,PN=3,ON=1,MN=OM-ON=2,
则S△AOP=S四边形OPAM-S△AOM=S△PON+S梯形AMNP-S△AOM
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4,
在△APB中,O为AB的中点,即AO=BO,
∴S△AOP=S△BOP,
同理S△BOQ=S△AOQ=S△AOP=S△BOP,
又∵S平行四边形APBQ=S△BOQ+S△AOQ+S△AOP+S△BOP,
∴S平行四边形APBQ=4S△AOP=16.
故答案为:(1)(-3,-1);(2)-3≤x<0或x≥3;(3)①平行四边形
点评:此题考查了反比例函数的综合题,涉及的知识有:对称的性质,反比例函数的性质,正比例函数与反比例函数的交点问题,坐标与图形性质,平行四边形的判定与性质,以及三角形、梯形面积的求法,利用了转化及数形结合的思想,其中当正比例函数与反比例函数要有交点,必然有两个,且两点关于原点对称,灵活运用此性质是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目