题目内容
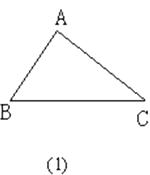
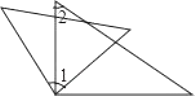
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE. 
(1)求证:△DEF是等腰三角形;
(2)求证:∠B=∠DEF;
(3)当∠A=40°时,求∠DEF的度数.
【答案】
(1)证明:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中, 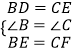 ,
,
∴△DBE≌△ECF,
∴DE=FE,
∴△DEF是等腰三角形
(2)证明:∵△BDE≌△CEF,
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B
(3)证明:∵由(2)知△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠CEF+∠DEF=∠BDE+∠B,
∴∠DEF=∠B,
∴AB=AC,∠A=40°,
∴∠DEF=∠B= ![]() =70°
=70°
【解析】(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;(2)根据△BDE≌△CEF,可知∠FEC=∠BDE,∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B即可得出结论;(3)由(2)知∠DEF=∠B,再根据等腰三角形的性质即可得出∠DEF的度数.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目