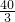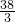题目内容
若用半径为r的圆形桌布将边长为60cm的正方形餐桌盖住，则r的最小值为 ________cm．
30
分析：依据桌布的直径等于正方形的对角线长，即可求解．
解答：边长为60 cm的正方形的对角线长=60，即圆的直径为60，
所以圆的半径的最小值为60÷2=30cm．
点评：本题利用了圆内接正方形的边长与圆半径的关系求解．
分析：依据桌布的直径等于正方形的对角线长，即可求解．
解答：边长为60 cm的正方形的对角线长=60
，即圆的直径为60，所以圆的半径的最小值为60
÷2=30cm．点评：本题利用了圆内接正方形的边长与圆半径的关系求解．
练习册系列答案
相关题目
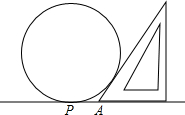为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得PA=5cm，求铁环的半径．
