题目内容
把两个半径为5和一个半径为8的圆形纸片放在桌面上,使它们两两外切,若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于分析:由题意作出图形,要求则这个大圆形纸片的最小半径,则在△APO中,将OA、OP分别用R表示后由勾股定理可得R值,即这个大圆形纸片的最小半径.
解答: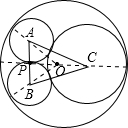 解:如图所示,⊙A、⊙B半径为5,⊙C半径为8,设⊙O半径为R.
解:如图所示,⊙A、⊙B半径为5,⊙C半径为8,设⊙O半径为R.
连接AB、BC、CA,则AB=10,BC=CA=13,过C作CP⊥AB,则P是AB中点.
∴AP=5,
在△ACP中由勾股定理CP2=AC2-AP2,
∴CP=12,
∵OC=R-8,
∴OP=20-R,
在△APO中,∵OA=R-5,AP=5,
∴由勾股定理AP2=AO2-OP2,
即52=(R-5)2-(20-R)2,
∴R=
,则这个大圆形纸片的最小半径等于
.
 解:如图所示,⊙A、⊙B半径为5,⊙C半径为8,设⊙O半径为R.
解:如图所示,⊙A、⊙B半径为5,⊙C半径为8,设⊙O半径为R.连接AB、BC、CA,则AB=10,BC=CA=13,过C作CP⊥AB,则P是AB中点.
∴AP=5,
在△ACP中由勾股定理CP2=AC2-AP2,
∴CP=12,
∵OC=R-8,
∴OP=20-R,
在△APO中,∵OA=R-5,AP=5,
∴由勾股定理AP2=AO2-OP2,
即52=(R-5)2-(20-R)2,
∴R=
| 40 |
| 3 |
| 40 |
| 3 |
点评:本题考查了相切圆的性质,以及勾股定理的应用,同学们应熟练掌握.

练习册系列答案
相关题目
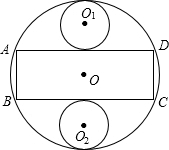 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
