题目内容
【题目】如图,抛物线![]() 与双曲线
与双曲线![]() 全相交于点A、B,且抛物线经过坐标原点,点
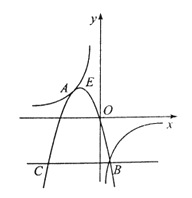
全相交于点A、B,且抛物线经过坐标原点,点![]() 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算![]() 与
与![]() 的面积;
的面积;
(3)在抛物线上是否存在点D,使![]() 的面积等于
的面积等于![]() 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() (2)15,
(2)15, ![]() (3) D的坐标为(3,﹣18)或(﹣4,﹣4)
(3) D的坐标为(3,﹣18)或(﹣4,﹣4)
【解析】解:(1)∵点A(﹣2,2)在双曲线![]() 上,
上,
∴k=﹣4。
∴双曲线的解析式为![]() 。
。
∵BC与x轴之间的距离是点B到y轴距离的4倍,
∴设B点坐标为(m,﹣4m)(m>0)代入双曲线解析式得m=1。
∴抛物线y=ax2+bx+c(a<0)过点A(﹣2,2)、B(1,﹣4)、O(0,0)。
∴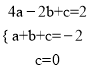 ,解得:
,解得: ![]() 。
。
∴抛物线的解析式为![]() 。
。
(2)∵抛物线的解析式为![]() ,
,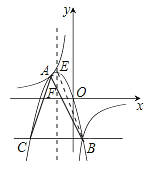
∴顶点E(![]() ),对称轴为x=
),对称轴为x=![]() 。
。
∵B(1,﹣4),∴﹣x2﹣3x=﹣4,解得:x1=1,x2=﹣4。
∴C(﹣4,﹣4)。
∴S△ABC=![]() ×5×6=15,
×5×6=15,
由A、B两点坐标为(﹣2,2),(1,﹣4)可求得直线AB的解析式为:y=﹣2x﹣2。
设抛物线的对称轴与AB交于点F,则F点的坐标为(![]() ,1)。
,1)。
∴EF=![]() 。∴S△ABE=S△AEF+S△BEF=
。∴S△ABE=S△AEF+S△BEF=![]() ×
×![]() ×3=
×3=![]() 。
。
(3)S△ABE=![]() ,∴8S△ABE=15。
,∴8S△ABE=15。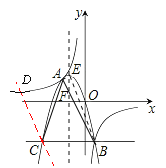
∴当点D与点C重合时,显然满足条件,
当点D与点C不重合时,过点C作AB的平行线CD,
其直线解析式为y=﹣2x﹣12。
令﹣2x﹣12=﹣x2﹣3x,解得x1=3,x2=﹣4(舍去)。
当x=3时,y=﹣18,故存在另一点D(3,﹣18)满足条件。
综上所述,可得点D的坐标为(3,﹣18)或(﹣4,﹣4)。
(1)将点A的坐标代入双曲线方程即可得出k的值,设B点坐标为(m,﹣4m)(m>0),根据双曲线方程可得出m的值,然后分别得出了A、B、O的坐标,利用待定系数法求解二次函数解析式即可。
(2)根据点B的坐标,结合抛物线方程可求出点C的坐标,从而可得出△ABC的面积。先求出AB的解析式,然后求出点F的坐标,及EF的长,从而根据S△ABE=S△AEF+S△BEF可得△ABE的面积。
(3)先确定符合题意的△ABD的面积,从而可得出当点D与点C重合时,满足条件;当点D与点C不重合时,过点C作AB的平行线CD,则可求出其解析式,求出其与抛物线的交点坐标即可得出点D的坐标。