Question

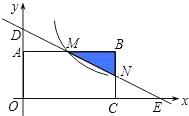
【题目】如图（1），在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），将线段AB先向上平移2个单位长度，再向右平移1个单位长度，得到线段CD，连接AC，BD，构成平行四边形ABDC．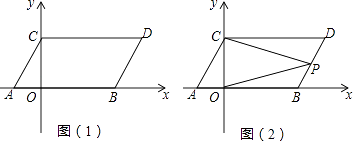

（1）请写出点C的坐标为 ， 点D的坐标为 ， S四边形ABDC；
（2）点Q在y轴上，且S△QAB=S四边形ABDC ， 求出点Q的坐标；
（3）如图（2），点P是线段BD上任意一个点（不与B、D重合），连接PC、PO，试探索∠DCP、∠CPO、∠BOP之间的关系，并证明你的结论．

Answer 1

【答案】
（1）（0，2）；（4，2）；8
（2）

解：∵点Q在y轴上，设Q（0，m），

∴OQ=|m|，

∴S△QAB= ×AB×OQ= ×4×|m|=2|m|，

∵S四边形ABDC=8，

∴2|m|=8，

∴m=4或m=﹣4，

∴Q（0，4）或Q（0，﹣4）

（3）

解：如图

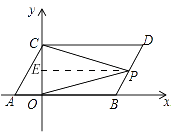
∵线段CD是线段AB平移得到，

∴CD∥AB，

作PE∥AB，

∴CD∥PE，

∴∠CPE=∠DCP，

∵PE∥AB，

∴∠OPE=∠BOP，

∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP，

∴∠CPO=∠DCP+∠BOP

【解析】解：（1）∵线段AB先向上平移2个单位长度，再向右平移1个单位长度，得到线段CD，
且（﹣1，0），B（3，0），
∴C（0，2），D（4，2）；
∵AB=4，OC=2，
∴S四边形ABDC=AB×OC=8；
所以答案是：（0，2）；（4，2）；8；
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分，以及对平行四边形的判定的理解，了解两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．