题目内容
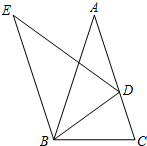 如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.(1)旋转中心是
(2)如果旋转角恰好是△ABC底角度数的
| 1 | 2 |
(3)△BDC是
分析:(1)确定图形的旋转时首先要确定旋转前后的对应点,即可确定旋转中心.
(2)根据题意可得出∠A=∠ABD=∠DBC=
∠C,从而根据三角形的内角和定理可得出答案.
(3)由外角定理可得出∠C=∠ADB,从而可判断出答案.
(2)根据题意可得出∠A=∠ABD=∠DBC=
| 1 |
| 2 |
(3)由外角定理可得出∠C=∠ADB,从而可判断出答案.
解答:解:(1)由图形及旋转的特点可得旋转中心是点B;
(2)∵旋转角恰好是△ABC底角度数的
,且AD=BD,
∴∠A=∠ABD=∠DBC=
∠C,
∴在△ABC中可求得∠DBC=36°.
(3)由(1)得:∠DBC=∠A+∠ABD=∠C.
∴△BDC是等腰三角形.
故答案为:B、36、等腰.
(2)∵旋转角恰好是△ABC底角度数的
| 1 |
| 2 |
∴∠A=∠ABD=∠DBC=
| 1 |
| 2 |
∴在△ABC中可求得∠DBC=36°.
(3)由(1)得:∠DBC=∠A+∠ABD=∠C.
∴△BDC是等腰三角形.
故答案为:B、36、等腰.
点评:本题考查等腰三角形的性质及旋转的性质,难度不大,解答本题的关键是根据图形得出旋转角及旋转中心.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
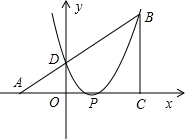 ,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.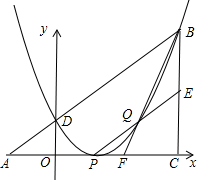 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D. 25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.
25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE. 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的. 如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.