Question

【题目】在平面直角坐标系xOy中，抛物线y=x2+bx+c经过点A(-1，t)，B(3，t)，与y轴交于点C(0，-1)．一次函数y=x+n的图象经过抛物线的顶点D．

（）求抛物线的表达式．

（）求一次函数的表达式．

（）将直线绕其与轴的交点旋转，使当时，直线总位于抛物线的下方，请结合函数图象，求的取值范围．

Answer 1

【答案】（1）y=x2-2x-1；（2）一次函数y=x+n的表达式是y=x-3；（3）当-5＜m＜1时，当-1≤x≤1时，直线l总位于抛物线的下方．

【解析】试题分析：（1）根据A和B对称，可求得对称轴，则b的值即可求得，然后根据函数经过点C(0,1).代入即可求得c的值，则抛物线解析式即可求得；
（2）首先求得抛物线的顶点，代入一次函数解析式即可求得n的值，求得一次函数的解析式；
（3）首先求得抛物线上当和时对应点的坐标，然后求得直线经过这两个点时对应的的值，据此即可求解．

试题解析：(1)二次函数的对称轴是

则

解得：b=2，

∵抛物线与y轴交于点C(0,1).

∴c=1，

则二次函数的解析式是；

(2)二次函数的顶点坐标是(1,2)，

代入y=x+n得2=1+n，

解得：n=3，

则一次函数y=x+n的表达式是y=x3；

(3)如图所示：

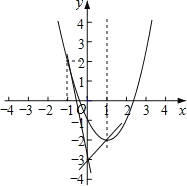
在中，当x=1时，y=2；

当x=1时，y=2.

当直线y=mx3经过点(1,2)时，m3=2，解得：m=5；

当直线y=mx3经过点(1,2)时，m3=2，解得：m=1.

则当5<m<1时，当时，直线l总位于抛物线的下方.