题目内容
如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD= ,∠C=45°,点P是BC边上一动点,设PB的长为x.
,∠C=45°,点P是BC边上一动点,设PB的长为x.
小题1:当x的值为____________时,以点P、A、D、E为顶点的四边形为直角梯形
小题2:当x的值为____________时,以点P、A、D、E为顶点的四边形为平行四边形;
小题3:点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
 ,∠C=45°,点P是BC边上一动点,设PB的长为x.
,∠C=45°,点P是BC边上一动点,设PB的长为x.小题1:当x的值为____________时,以点P、A、D、E为顶点的四边形为直角梯形
小题2:当x的值为____________时,以点P、A、D、E为顶点的四边形为平行四边形;
小题3:点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.

小题1:3或8
小题2:1或11
小题3:由(2)知,当BP=11时,以P、A、D、E为顶点的四边形为菱形
解:(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
∴AM=DN,AD=MN=5,
而CD=4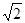 ,∠C=45°,
,∠C=45°,
∴DN=CN=4=AM,
∴BM=CB-CN-MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DEB=90°时,
∴P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,有两种情况:
①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE-PE=6-5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形
∴EP=AD=5,
过D作DN⊥BC于N,
∵CD=4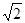 ,∠C=45°,
,∠C=45°,
则DN=CN=4,
∴NP=3.
∴DP=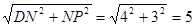
∴EP=DP,
故此时?PDAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形
∴AM=DN,AD=MN=5,
而CD=4
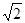 ,∠C=45°,
,∠C=45°,∴DN=CN=4=AM,
∴BM=CB-CN-MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DEB=90°时,
∴P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,有两种情况:
①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE-PE=6-5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形
∴EP=AD=5,
过D作DN⊥BC于N,
∵CD=4
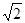 ,∠C=45°,
,∠C=45°,则DN=CN=4,
∴NP=3.
∴DP=
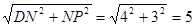
∴EP=DP,
故此时?PDAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形

练习册系列答案
相关题目

 ABD的周长为l6cm,则
ABD的周长为l6cm,则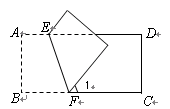


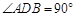 ,CA = 10,DB = 6,OE⊥AC于点O,连结CE,则△CBE的周长是_________.
,CA = 10,DB = 6,OE⊥AC于点O,连结CE,则△CBE的周长是_________.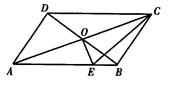
 中,
中,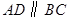 ,
,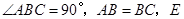 为
为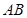 边上一点,
边上一点,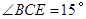 ,且
,且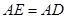 .连接
.连接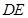 交对角线
交对角线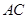 于
于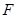 ,连接
,连接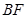 .下列结论:
.下列结论: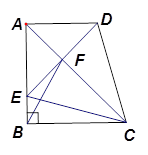
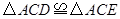 ;②
;②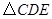 为等边三角形;
为等边三角形;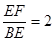 ;④
;④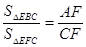 . 其中结论正确的是
. 其中结论正确的是