题目内容
已知在平面直角坐标系xoy中,二次函数y=-2x²+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
(1)y=-2x2-4x+6;(2)sin∠ABD=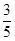 ;(3)略.
;(3)略.
解析试题分析:(1)把点A、B的坐标代入函数解析式计算求出b、c的值,即可得解;
(2)先求出抛物线的顶点坐标,再根据向右平移横坐标加,求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0),然后利用待定系数法求出直线BC的解析式,再求出与x轴的交点D的坐标,过点A作AH⊥BD于H,先求出OD,再利用勾股定理列式求出BD,然后求出△ADH和△BDO相似,利用相似三角形对应边成比例列式求出AH,再利用勾股定理,然后根据锐角的正弦等于对边比斜边列式计算即可得解;
(3)过点C作CP⊥x轴于P,分别求出∠BAO和∠COP的正切值,根据正切值相等求出∠BAO=∠COP,再根据同位角相等,两直线平行解答.
试题解析:(1)由题意得, ?2×9?3b+c=0 c=6 ,
解得 b=?4 c=6 ,
所以,此二次函数的解析式为y=-2x2-4x+6;
(2)∵y=-2x2-4x+6=-2(x+1)2+8,
∴函数y=2x2-4x+6的顶点坐标为(-1,8),
∴向右平移5个单位的后的顶点C(4,8),
设直线BC的解析式为y=kx+b(k≠0),
则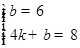 ,
,
解得 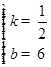 ,
,
所以,直线BC的解析式为y=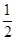 x+6,
x+6,
令y=0,则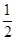 x+6=0,
x+6=0,
解得x=-12,
∴点D的坐标为(-12,0),
过点A作AH⊥BD于H,
OD=12,BD=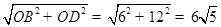 ,
,
AD=-3-(-12)=-3+12=9,
∵∠ADH=∠BDO,∠AHD=∠BOD=90°,
∴△ADH∽△BDO,
∴AH:OB ="AD:BD" ,
即AH:6 =9: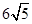 ,
,
解得AH=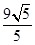 ,
,
∵AB=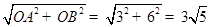 ,
,
∴sin∠ABD=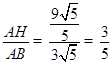 ;
;
(3)过点C作CP⊥x轴于P,
由题意得,CP=8,PO=4,AO=3,BO=6,
∴tan∠COP=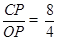 =2,
=2,
tan∠BAO= =2,
=2,
∴tan∠COP=tan∠BAO,
∴∠BAO=∠COP,
∴AB∥OC.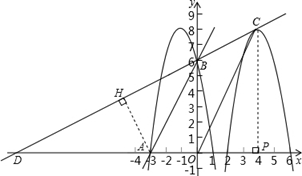
考点:二次函数综合题.


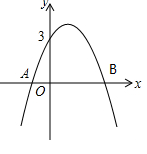
 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
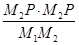 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
 经过A(
经过A( ,0)、B(5,0)两点,顶点为P.
,0)、B(5,0)两点,顶点为P. ,
, )和点D(
)和点D( ,
, )在该抛物线上,则当
)在该抛物线上,则当 时,
时, ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题: