题目内容
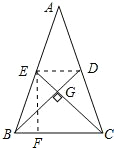
如图,在△ABC中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则tan∠ABC=______.


如图,连接DE,过E点作EF⊥BC,垂足为F,
设DE=2x,
依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=
(BC-DE)=x,则FC=3x,
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,
∴tan∠ABC=
=
=3.
故本题答案为:3.
设DE=2x,
依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=
| 1 |
| 2 |
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,
∴tan∠ABC=
| EF |
| BF |
| 3x |
| x |
故本题答案为:3.


练习册系列答案
相关题目
