题目内容
已知n是正整数,pn(xn,yn)是反比例函数y=| k | x |
T1=x1y2,T2=x2y3,…,T8=x8y9;若T1=1,则T1•T2•…•T8的值是
分析:由于pn(xn,yn)是反比例函数y=
的图象上的一列点,则k=xn•yn,T1•T2•…•T8=x1(y2•x2)(y3•x3)…(y8•x8)y9=
,又T1=1,求得k值,代入即可.
| k |
| x |
| k8 |
| 9 |
解答:解:pn(xn,yn)是反比例函数y=
的图象上的一列点,则k=xn•yn,
又x1=1,x2=2,…,xn=n,T1=x1y2,T2=x2y3,…,T8=x8y9,T1=1,
则y2=1,k=x2•y2=2,T1•T2•…•T8=x1(y2•x2)(y3•x3)…(y8•x8)y9=
=
.
故答案为
.
| k |
| x |
又x1=1,x2=2,…,xn=n,T1=x1y2,T2=x2y3,…,T8=x8y9,T1=1,
则y2=1,k=x2•y2=2,T1•T2•…•T8=x1(y2•x2)(y3•x3)…(y8•x8)y9=
| k8 |
| 9 |
| 256 |
| 9 |
故答案为
| 256 |
| 9 |
点评:此题难度稍大,题目新颖,但仍旧考查的是反比例函数图象上点的坐标特征,重点是k的取值.

练习册系列答案
相关题目
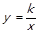 图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,T9=x9y10;若T1=1,则T1·T2·T3…T9的值是_________
图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,T9=x9y10;若T1=1,则T1·T2·T3…T9的值是_________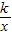 图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,Tn=xnyn+1;若T1=1,则T1•T2•…•Tn= .
图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,Tn=xnyn+1;若T1=1,则T1•T2•…•Tn= .