题目内容
已知n是正整数,Pn(xn,yn)是反比例函数y=| k | x |
分析:根据反比例函数图象上点的坐标特征解答.
解答:解:T1•T2•…•Tn=x1y2•x2y3…xnyn+1=x1•
•x2•
•x3•
…xn•
=x1•
,
又因为x1=1,
所以原式=
,
又因为T1=1,所以x1y2=1,又因为x1=1,所以y2=1,即
=1,又x2=2,k=2,
T1=1时,于是T1•T2•…•Tn=
,
∵xn=n+1,
∴原式=
.
故答案为:
.
| k |
| x2 |
| k |
| x3 |
| k |
| x4 |
| k |
| xn+1 |
| kn |
| xn+1 |
又因为x1=1,
所以原式=
| kn |
| xn+1 |
又因为T1=1,所以x1y2=1,又因为x1=1,所以y2=1,即
| k |
| x2 |
T1=1时,于是T1•T2•…•Tn=
| 2n |
| xn+1 |
∵xn=n+1,
∴原式=
| 2n |
| n+1 |
故答案为:
| 2n |
| n+1 |
点评:解答此题的关键是将x1•
•x2•
•x3•
…xn•
的相同字母消掉,使原式化简为一个仅含k的代数式,然后解答.
| k |
| x2 |
| k |
| x3 |
| k |
| x4 |
| k |
| xn+1 |

练习册系列答案
相关题目
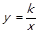 图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,T9=x9y10;若T1=1,则T1·T2·T3…T9的值是_________
图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,T9=x9y10;若T1=1,则T1·T2·T3…T9的值是_________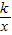 图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,Tn=xnyn+1;若T1=1,则T1•T2•…•Tn= .
图象上的一列点,其中x1=1,x2=2,…,xn=n,记T1=x1y2,T2=x2y3,…,Tn=xnyn+1;若T1=1,则T1•T2•…•Tn= .