题目内容
如图,直角三角形ABC中,∠C=90°,∠A=30°,点O在斜边AB上,半径为2的⊙O过点B,且切AC边于点D,交BC边于点E,

求:(1)弧DE的长; (结果保留π)
(2)由线段CD,CE及弧DE围成的阴影部分的面积。(结果保留π和根号)

求:(1)弧DE的长; (结果保留π)
(2)由线段CD,CE及弧DE围成的阴影部分的面积。(结果保留π和根号)
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)连接OD、OE,一方面根据切线的性质和直角三角形两锐角的关系求得∠AOD=600,另一方面根据等边三角形的判定和性质得出∠BOE =600,从而求得∠DOE =600,根据弧长公式即可求得DE弧长;
(2)用梯形OECD和扇形ODE的面积差来求出阴影部分的面积.
试题解析:(1)如图,连接OD、OE,
∵AC是⊙O的切线,∴OD⊥AC,即∠ADO=90°.
∵∠C=90°,∠A=30°,OD=2,∴OA=4,∠AOD=∠B=600.
又∵OB=OE,∴△OBE是等边三角形. ∴∠BOE =600. ∴∠DOE =600.
∴DE弧长为
 .
.(2)∵∠C=90°,∠A=30°,OD=2,∴OA="4." ∴AB="6." ∴BC="3" ,AC=3
 ,AD=2
,AD=2 ,CD=
,CD= .
.∴
 .
.

练习册系列答案
相关题目

 cm,侧面展开图是半圆.
cm,侧面展开图是半圆.
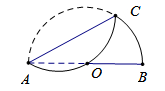
 ,∠AOC=( )
,∠AOC=( )