��Ŀ����
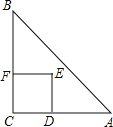
����Ŀ����ͼ�ף�AB��BD��CD��BD��AP��PC������ֱ�ΪB��P��D��������������ͬһֱ���ϣ����ǰ�������ͼ�νС�����ͼ����
��1��֤����ABCD=PBPD��
��2����ͼ�ң�Ҳ��һ��������ͼ�����������۳�������˵�����ɣ�
��3����֪��������x�ύ�ڵ�A��-1��0����B��3��0������y�ύ�ڵ㣨0��-3��������ΪP����ͼ����ʾ����Q��������������A��B��P�ĵ㣬ʹ�á�QAP=90������Q�����꣮

���𰸡���1����2������������3����![]() ��
�� ![]() ����
����
�������������������1������ͬ�ǵ������������A=��CPD��Ȼ�������ABP�͡�PCD���ƣ��ٸ������������ζ�Ӧ�߳ɱ�����ʽ�������ɵ�֤��
��2���루1����֤��˼·��ͬ��
��3�����ô���ϵ����������κ�������ʽ�����������߽���ʽ�����P�����꣬�ٹ���P��PC��x����C����AQ��y���ཻ��D��Ȼ�����PC��AC�ij����ٸ��ݣ�2���Ľ������OD�ij����Ӷ��õ���D�����꣬���ô���ϵ�������ֱ��AD�Ľ���ʽ���������߽���ʽ������⼴�ɵõ���Q�����꣮
���������
��1��֤������AB��BD��CD��BD��
���B=��D=90����
���A+��APB=90����
��AP��PC��
���APB+��CPD=90����
���A=��CPD��
���ABP�ס�PCD��
��![]() ��
��
��ABCD=PBPD��
��2��ABCD=PBPD��Ȼ������
�������£���AB��BD��CD��BD��
���B=��CDP=90����
���A+��APB=90����
��AP��PC��
���APB+��CPD=90����
���A=��CPD��
���ABP�ס�PCD��
��![]() ��
��
��ABCD=PBPD��
��3���������߽���ʽΪ![]() ��a��0����
��a��0����
����������x�ύ�ڵ�A��-1��0����B��3��0������y�ύ�ڵ㣨0��-3����
��![]() �� �ѣ�0��-3������
�� �ѣ�0��-3������
�� y=x2-2x-3��
��y=x2-2x-3=��x-1��2-4��
�ඥ��P������Ϊ��1��-4����
����P��PC��x����C������Q��x�������ߣ�����ΪE.
��QE=m���ɵ�(2)����۵�AE=2m����Q������Ϊ��2m -1��m������y=x2-2x-3��
���m=![]() ��m=0����ȥ������y=
��m=0����ȥ������y=![]() ����y=x2-2x-3�����x=
����y=x2-2x-3�����x=![]() ��x=
��x=![]() ����ȥ��
����ȥ��
���Q��������![]() ��
�� ![]() ��
��