题目内容
 如图,一次函数y=ax-1的图象与反比例函数y=
如图,一次函数y=ax-1的图象与反比例函数y=| k |
| x |
| 10 |
| 1 |
| 3 |
(1)求a,k的值及点B的坐标;
(2)观察图象,请直接写出不等式ax-1≥
| k |
| x |
(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
考点:反比例函数综合题
专题:综合题
分析:(1)过A作AE⊥x轴,交x轴于点E,在Rt△AOE中,根据tan∠AOC的值,设AE=x,得到OE=3x,再由OA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出A坐标,将A坐标代入一次函数解析式求出a的值,代入反比例解析式求出k的值,联立一次函数与反比例函数解析式求出B的坐标;
(2)由A与B交点横坐标,根据函数图象确定出所求不等式的解集即可;
(3)显然P与O重合时,满足△PDC与△ODC相似;当PC⊥CD,即∠PCD=90°时,满足三角形PDC与三角形CDO相等,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形PCO与三角形CDO相似,由相似得比例,根据OD,OC的长求出OP的长,即可确定出P的坐标.
(2)由A与B交点横坐标,根据函数图象确定出所求不等式的解集即可;
(3)显然P与O重合时,满足△PDC与△ODC相似;当PC⊥CD,即∠PCD=90°时,满足三角形PDC与三角形CDO相等,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形PCO与三角形CDO相似,由相似得比例,根据OD,OC的长求出OP的长,即可确定出P的坐标.
解答: 解:(1)过A作AE⊥x轴,交x轴于点E,
解:(1)过A作AE⊥x轴,交x轴于点E,
在Rt△AOE中,OA=
,tan∠AOC=
,
设AE=x,则OE=3x,
根据勾股定理得:OA2=OE2+AE2,即10=9x2+x2,
解得:x=1或x=-1(舍去),
∴OE=3,AE=1,即A(3,1),
将A坐标代入一次函数y=ax-1中,得:1=3a-1,即a=
,
将A坐标代入反比例解析式得:1=
,即k=3,
联立一次函数与反比例解析式得:
,
消去y得:
x-1=
,
解得:x=-
或x=3,
将x=-
代入得:y=-1-1=-2,即B(-
,-2);
(2)由A(3,1),B(-
,-2),
根据图象得:不等式
x-1≥
的解集为-
≤x<0或x≥3;
(3)显然P与O重合时,△PDC∽△ODC;
当PC⊥CD,即∠PCD=90°时,∠PCO+∠DCO=90°,
∵∠PCD=∠COD=90°,∠PCD=∠CDO,
∴△PDC∽△CDO,
∵∠PCO+∠CPO=90°,
∴∠DCO=∠CPO,
∵∠POC=∠COD=90°,
∴△PCO∽△CDO,
∴
=
,
对于一次函数解析式y=
x-1,令x=0,得到y=-1;令y=0,得到x=
,
∴C(
,0),D(0,-1),即OC=
,OD=1,
∴
=
,即OP=
,
此时P坐标为(0,
),
综上,满足题意P的坐标为(0,
)或(0,0).
 解:(1)过A作AE⊥x轴,交x轴于点E,
解:(1)过A作AE⊥x轴,交x轴于点E,在Rt△AOE中,OA=
| 10 |
| 1 |
| 3 |
设AE=x,则OE=3x,
根据勾股定理得:OA2=OE2+AE2,即10=9x2+x2,
解得:x=1或x=-1(舍去),
∴OE=3,AE=1,即A(3,1),
将A坐标代入一次函数y=ax-1中,得:1=3a-1,即a=
| 2 |
| 3 |
将A坐标代入反比例解析式得:1=
| k |
| 3 |
联立一次函数与反比例解析式得:
|
消去y得:
| 2 |
| 3 |
| 3 |
| x |
解得:x=-
| 3 |
| 2 |
将x=-
| 3 |
| 2 |
| 3 |
| 2 |
(2)由A(3,1),B(-
| 3 |
| 2 |
根据图象得:不等式
| 2 |
| 3 |
| 3 |
| x |
| 3 |
| 2 |
(3)显然P与O重合时,△PDC∽△ODC;
当PC⊥CD,即∠PCD=90°时,∠PCO+∠DCO=90°,
∵∠PCD=∠COD=90°,∠PCD=∠CDO,
∴△PDC∽△CDO,
∵∠PCO+∠CPO=90°,
∴∠DCO=∠CPO,
∵∠POC=∠COD=90°,
∴△PCO∽△CDO,
∴
| CO |
| DO |
| PO |
| CO |
对于一次函数解析式y=
| 2 |
| 3 |
| 3 |
| 2 |
∴C(
| 3 |
| 2 |
| 3 |
| 2 |
∴
| ||
| 1 |
| PO | ||
|
| 9 |
| 4 |
此时P坐标为(0,
| 9 |
| 4 |
综上,满足题意P的坐标为(0,
| 9 |
| 4 |
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法确定函数解析式,一次函数与反比例函数的交点问题,坐标与图形性质,勾股定理,锐角三角函数定义,相似三角形的判定与性质,利用了数形结合的思想,熟练运用数形结合思想是解本题第二问的关键.

练习册系列答案
相关题目
 已知一次函数y=kx+b(k≠0)的图象经过点(1,1)和点(0,-1).
已知一次函数y=kx+b(k≠0)的图象经过点(1,1)和点(0,-1).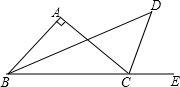 已知:如图,△ABC中,∠B的平分线和△ABC的外角平分线交于点D,∠A=90°.求∠D的度数.
已知:如图,△ABC中,∠B的平分线和△ABC的外角平分线交于点D,∠A=90°.求∠D的度数.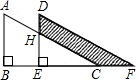 如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.
如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.