题目内容
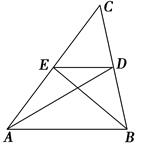
在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有__________条.


3
根据相似三角形的判定方法分别利用平行线以及垂直平分线的性质得出对应角相等即可得出.
解:当PD∥BC时,△APD∽△ABC,
当PE∥AC时,△BPE∽△BAC,
连接PC,

∵∠A=36°,AB=AC,点P在AC的垂直平分线上,
∴AP=PC,∠ABC=∠ACB=72°,
∴∠ACP=∠PAC=36°,
∴∠PCB=36°,
∴∠B=∠B,∠PCB=∠A,
∴△CPB∽△ACB,
故过点P的△ABC的相似线最多有3条.
故答案为:3.
解:当PD∥BC时,△APD∽△ABC,
当PE∥AC时,△BPE∽△BAC,
连接PC,

∵∠A=36°,AB=AC,点P在AC的垂直平分线上,
∴AP=PC,∠ABC=∠ACB=72°,
∴∠ACP=∠PAC=36°,
∴∠PCB=36°,
∴∠B=∠B,∠PCB=∠A,
∴△CPB∽△ACB,
故过点P的△ABC的相似线最多有3条.
故答案为:3.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

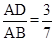 ,则EC的长是( )
,则EC的长是( )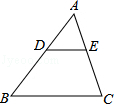
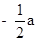 B.
B.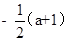 C.
C.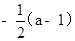 D.
D.