题目内容
【题目】已知,直线l过点(2,2)和(-2,0).
(1)求出直线![]() 的函数解析式;
的函数解析式;
(2)画出直线![]() 的函数图象;
的函数图象;
(3)根据函数图象,直接写出y<2时x的取值范围.
【答案】(1)![]() ;
;
(2)函数图像见详解;
(3)当y<2时,x<2;
【解析】
(1)设一次函数的解析式为![]() ,将点(2,2)和(-2,0),代入得
,将点(2,2)和(-2,0),代入得![]() ,即可求得解析式;
,即可求得解析式;
(2)根据点(2,2)和(-2,0)可以作出函数图像,
(3)由点(2,2)可知,当y=2时,x=2,并且函数图像y随x的增大而增大,可知当y<2时,x<2;
解:(1)设一次函数的解析式为![]() ,因为经过点(2,2)和(-2,0),代入得:
,因为经过点(2,2)和(-2,0),代入得:![]() ,解之得:
,解之得:![]()
所以解析式为![]() ;
;
(2)根据点(2,2)和(-2,0)可以作出函数图像,如下图所示:
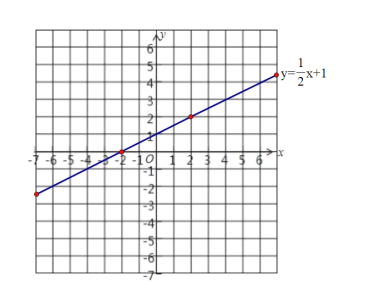
(3)由点(2,2)可知,当y=2时,x=2,并且由图可知,函数图像y随x的增大而增大,可知当y<2时,x<2;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为“厉行节能减排,倡导绿色出行”,某公司拟在我县甲、乙两个街道社区试点投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型,投放情况如下表:
成本单价 (单位:元) | 投放数量(单位:辆) | 总价(单位:元) | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合计(单位:元) | 7500 | ||
(1)根据表格填空:
本次试点投放的A、B型“小黄车”共有 辆;用含有![]() 的式子表示出B型自行车的成本总价为 ;
的式子表示出B型自行车的成本总价为 ;
(2)试求A、B两种款型自行车的单价各是多少元?
(3)经过试点投放调查,现在该公司决定采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.






