Question

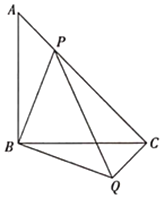
【题目】如图，等腰直角中，，点在上，将绕顶点沿顺时针方向旋转90°后得到.

（1）求的度数；

（2）当，时，求的大小；

（3）当点在线段上运动时（不与，重合），求证：.

Answer 1

【答案】（1）；（2）；（3）见解析.

【解析】

（1）由于∠PCB=∠BCQ=45°，故有∠PCQ=90°;

（2）利用勾股定理得出AC的长，再利用旋转的性质得出AP=CQ，求得PC的长度，进而利用勾股定理得出PQ的长；

（3）先证明△PBQ也是等腰直角三角形，从而得到PQ2=2PB2=PA2+PC2．

（1）∵△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ，

∴，

∴，

∴.

（2）当时，有，，

，

∴.

（3）由（1）可得，，，

，

∴是等腰直角三角形，是直角三角形.

∴，

∵，

∴，

故有.