题目内容
【题目】如图,在ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O. 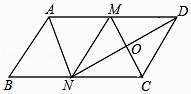
(1)求证:△ABN≌△CDM;
(2)连接MN,求证四边形MNCD是菱形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,
 ,
,
∴△ABN≌△CDM(SAS)
(2)证明:
∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC ![]() DM,
DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形
【解析】(1)由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,又由M、N分别是AD,BC的中点,即可利用SAS证得△ABN≌△CDM;(2)利用直角三角形形的性质结合菱形的判定方法证明即可.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目