题目内容
【题目】如图，折叠长方形的一边AD，使点D落在BC边上的点F处，BC=10cm，AB=8cm，求：
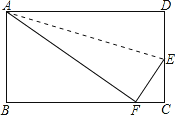
（1）EC的长；
（2）AE的长．
【答案】（1）3cm；（2）
cm.
【解析】
试题分析：（1）首先根据勾股定理求出BF的长，借助翻转变换的性质及勾股定理求出DE的长即可解决问题．
（2）直接根据勾股定理求出AE的长．
试题解析：（1）∵四边形ABCD为长方形，
∴AD=BC=10，DC=AB=8；
由题意得：△ADE≌△AFE，
∴AF=AD=10，EF=ED（设为x），
则EC=8-x；
在直角△ABF中，
由勾股定理得：
BF=
=6，
∴FC=10-6=4；
在直角△EFC中，
由勾股定理得：
x2=42+（8-x）2，
解得：x=5，8-x=3；
∴EC的长为3（cm）．
（2）由勾股定理得：
AE=
（cm）．
互动课堂系列答案
激活思维智能训练课时导学练系列答案【题目】某商场试销一种商品，成本为每件200元，规定试销期间销售单价不低于成本单价，且获利不得高于50%，一段时间后，发现销售量y（件）与销售单价x（元）之间的函数关系如下表：
销售单价x（元） | … | 230 | 235 | 240 | 245 | … |
销售量y（件） | … | 440 | 430 | 420 | 410 | … |
（1）请根据表格中所给数据，求出y关于x的函数关系式；
（2）设商场所获利润为w元，将商品销售单价定为多少时，才能使所获利润最大？最大利润是多少？
【题目】某校为实施国家“营养计划”工程，食堂用甲、乙两种原料配制成某种营养食品，已知这两种原料的维生素C含量及购买这两种原料的价格如下表：
| 甲种原料 | 乙种原料 |
维生素C（单位/千克） | 600 | 400 |
原料价格（元/千克） | 9 | 5 |
现要配制这种营养食品20千克，要求每千克至少含有480单位的维生素C．设购买甲种原料x千克．
（1）至少需要购买甲种原料多少千克？
（2）设食堂用于购买这两种原料的总费用为y元，求y与x的函数关系式，并说明购买甲种原料多少千克时，总费用最少？
