Question

【题目】已知：如图，点是的边上的一点，过点作，，，为垂足，再过点作，交于点，且．

（1）求证：；

（2）求证：垂直平分．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）连接BD，先根据DE⊥AB，DF⊥BC且DE=DF可知∠ABD=∠DBC，再根据DG∥AB即可得出∠ABD=∠BDG，进而可得出∠BDG=∠DBC，由等角对等边可知DG=BG；

（2）先根据（1）中∠ABD=∠DBC可知∠EDB=∠FDB，由全等三角形的判定定理可得出△BDE≌△BDF，再根据全等三角形的性质可得出BE=BF，DE=DF，故可得出BD垂直平分EF．

证明：（1）连接BD．

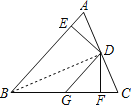
∵DE⊥AB，DF⊥BC且DE=DF，

∴∠ABD=∠DBC，

又∵DG∥AB，

∴∠ABD=∠BDG，

∴∠BDG=∠DBC，

∴DG=BG；

（2）由（1）∠ABD=∠DBC可知，∠EDB=∠FDB，

在△BDE与△BDF中，

∵∠ABD=∠DBC，BD=BD，∠EDB=∠FDB，

∴△BDE≌△BDF，

∴BE=BF，DE=DF，

∴BD垂直平分EF．