Question

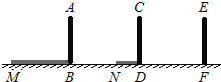
【题目】如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．

（1）求证：PA是⊙O的切线；

（2）若PD=，求⊙O的直径．

Answer 1

【答案】（1）证明见解析；（2）⊙O的直径为．

【解析】

试题分析：（1）连接OA，根据圆周角定理求出∠AOC，再由OA=OC得出∠ACO=∠OAC=30°，再由AP=AC得出∠P=30°，继而由∠OAP=∠AOC﹣∠P，可得出OA⊥PA，从而得出结论；

（2）利用含30°的直角三角形的性质求出OP=2OA，可得出OP﹣PD=OD，再由PD=，可得出⊙O的直径．

（1）证明：连接OA，

∵∠B=60°，

∴∠AOC=2∠B=120°，

又∵OA=OC，

∴∠OAC=∠OCA=30°，

又∵AP=AC，

∴∠P=∠ACP=30°，

∴∠OAP=∠AOC﹣∠P=90°，

∴OA⊥PA，

∴PA是⊙O的切线．

（2）在Rt△OAP中，∵∠P=30°，

∴PO=2OA=OD+PD，

又∵OA=OD，

∴PD=OA，

∵，

∴．

∴⊙O的直径为．