题目内容
【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
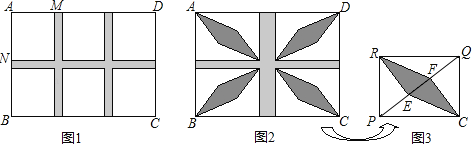
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.
【答案】(1)通道的宽是1m;(2)花坛RECF的面积为13.44m2.
【解析】
试题分析:(1)利用AM:AN=8:9,设通道的宽为xm,AM=8ym,则AN=9y,进而利用AD为18m,宽AB为13m得出等式求出即可;
(2)根据题意得出纵向通道的宽为2m,横向通道的宽为1m,进而得出PQ,RE的长,即可得出PE、EF的长,进而求出花坛RECF的面积.
解:(1)设通道的宽为xm,AM=8ym,
∵AM:AN=8:9,
∴AN=9y,
∴![]() ,
,
解得:![]() .
.
答:通道的宽是1m;
(2)∵四块相同草坪中的每一块,有一条边长为8m,若RP=8,则AB>13,不合题意,
∴RQ=8,
∴纵向通道的宽为2m,横向通道的宽为1m,
∴RP=6,
∵RE⊥PQ,四边形RPCQ是长方形,
∴PQ=10,
∴RE×PQ=PR×QR=6×8,
∴RE=4.8,
∵RP2=RE2+PE2,
∴PE=3.6,
同理可得:QF=3.6,
∴EF=2.8,
∴S四边形RECF=4.8×2.8=13.44,
即花坛RECF的面积为13.44m2.

练习册系列答案
相关题目