题目内容
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 的中点,点
的中点,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,到点
运动,到点![]() 停止,以
停止,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,
,![]() 为斜边
为斜边![]() 的中点,则点
的中点,则点![]() 运动的路程为______.
运动的路程为______.
【答案】![]()
【解析】
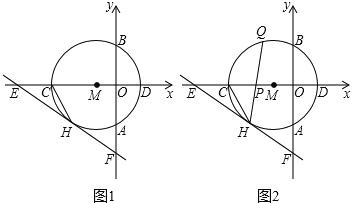
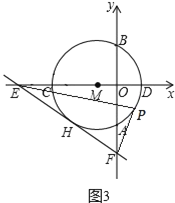
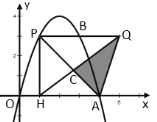
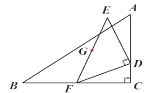
以点C为坐标原点建立坐标系,过点E作EH⊥y轴于H,利用AAS证出△EDH≌△DFC,从而得出AE=CD,DH=FC=4,设CD=a,由题意可知:0≤a≤6,则AE=a,CH=CD+DH=a+4,用a表示出点G的坐标,从而求出点G运动轨迹,然后根据平面直角坐标系中任意两点之间的距离公式计算即可.
解:如图,以点C为坐标原点建立坐标系,过点E作EH⊥y轴于H

∴∠EHD=∠DCF=90°
∴∠DFC+∠FDC=90°
∵![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 的中点,
的中点,
∴AC=![]() =6,CF=
=6,CF=![]()
∵△DEF为等腰直角三角形
∴DE=FD,∠EDF=90°
∴∠EDH+∠FDC=90°
∴∠EDH=∠DFC
在△EDH和△DFC中
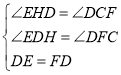
∴△EDH≌△DFC
∴AE=CD,DH=FC=4
设CD=a,由题意可知:0≤a≤6,则AE=a,CH=CD+DH=a+4
∴点E的坐标为(-a,a+4),点F坐标为(-4,0)
∵![]() 为斜边
为斜边![]() 的中点,
的中点,
∴点G的坐标为(![]() ,
,![]() )
)
令x=![]() ,y=
,y=![]()
解得:a=-2x-4,a=2y-4
∴-2x-4=2y-4
整理,得y=-x,即点G的运动轨迹为直线y=-x的一部分
∵0≤a≤6,
∴0≤-2x-4≤6,
∴-5≤x≤-2
当x=-2时,解得y=2,此时点G坐标为(-2,2);
当x=-5时,解得y=5,此时点G坐标为(-5,5)
∴![]() 运动的路程为
运动的路程为![]()
故答案为:![]() .
.

练习册系列答案
相关题目