Question

已知，等腰Rt△ABC中，点O是斜边的中点，△MPN是直角三角形，固定△ABC，滑动△MPN，在滑动过程中始终保持点P在AC上，且PE⊥AB，PF⊥BC，垂足分别为E、F．
（1）如图1，当点P与点O重合时，OE、OF的数量和位置关系分别是

 

．
（2）当△MPN移动到图2的位置时，（1）中的结论还成立吗？请说明理由．
（3）如图3，等腰Rt△ABC的腰长为6，点P在AC的延长线上时，Rt△MPN的边PM与AB的延长线交于点E，直线BC与直线NP交于点F，OE交BC于点H，且 EH：HO=2：5，则BE的长是多少？

Answer 1

分析：（1）根据题意及图示即可得出OE、OF的数量关系：相等，位置关系：垂直；
（2）根据题意及图示可证明△OEB≌△OFC，故成立；
（3）根据题意及图示，还有所给比例关系即可得出答案．

解答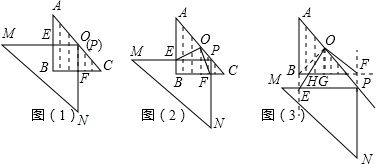：解：（1）数量关系：相等，位置关系：垂直
故答案为相等且垂直．

（2）成立，理由如下：
∵△MPN是直角三角形，
∴∠MPN=90°．
连接OB，
∴∠OBE=∠C=45°，
∵△ABC，△MPN是直角三角形，PE⊥AB，PF⊥BC，
∴∠ABC=∠MPN=∠BEP=∠BFP=90°，
∴四边形EBFP是矩形，
∴BE=PF
∵PF=CF，
∴BE=CF，
∵OB=OC=

1

2

AC，
∴在△OEB和△OFC中，

BE=CF ∠OBE=∠OCF OB=OC

∴△OEB≌△OFC（SAS），故成立，

（3）如图，找BC的中点G，连接OG，
∵O是AC中点，
∴OG∥AB，OG=

1

2

AB，
∵AB=6，
∴OG=3，
∵OG∥AB，
∴△BHE∽△GOH，
∵EH：HO=2：5，
∴BE：OG=2：5，
而OG=

1

2

AB=3，
∴BE=

6

5

．

点评：本题主要考查了等腰直角三角形的性质，全等三角形的证明，比例关系等，难度较大．