题目内容
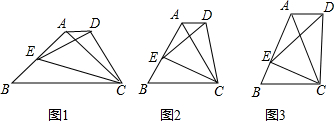
已知:等腰Rt△ABC中,∠A=90°,(1)如图1,E为AB上任意一点,以CE为斜边作等腰Rt△CDE,连接AD,则有AD∥BC;
(2)若将等腰Rt△ABC改为正△ABC,如图2所示,E为AB边上任一点,△CDE为正三角形,连接AD,上述结论还成立吗?答
(3)若△ABC为任意等腰三角形,AB=AC,如图3,E为AB上任一点,△DEC∽△ABC,连接AD,请问AD与BC的位置关系怎样?
 答:
答:请你在上述3个结论中,任选一个结论进行证明.
分析:欲证AD∥BC,可以根据等腰直角三角形,正三角形,等腰三角形的性质,证明△ACD∽△BCE,再证明AD与BC的内错角相等,得出结论.
解答:解:(1)∵△ABC和△DEC是等腰直角三角形,
∴△ABC∽△DEC,∠ACB=∠DCE=45°.
∴
=
,∠DCA=∠ECB.
∴△ACD∽△BCE.
∴∠DAC=∠EBC=45°.
∴∠DAC=∠ACB.
∴AD∥BC.
(2)∵△ABC和△DEC是正三角形,
∴△ABC∽△DEC,∠ACB=∠DCE=60°.
∴
=
,∠DCA=∠ECB.
∴△ACD∽△BCE.
∴∠DAC=∠EBC=60°.
∴∠DAC=∠ACB.
∴AD∥BC.
成立.
(3)∵△ABC是等腰三角形、△DEC是等腰直角三角形,△ABC∽△DEC,
∴∠ACB=∠DCE.
∴
=
,∠DCA=∠ECB.
∴△ACD∽△BCE.
∴∠DAC=∠EBC.
∴∠DAC=∠ACB.
∴AD∥BC.
∴△ABC∽△DEC,∠ACB=∠DCE=45°.
∴
| AC |
| BC |
| DC |
| EC |
∴△ACD∽△BCE.
∴∠DAC=∠EBC=45°.
∴∠DAC=∠ACB.
∴AD∥BC.
(2)∵△ABC和△DEC是正三角形,
∴△ABC∽△DEC,∠ACB=∠DCE=60°.
∴
| AC |
| BC |
| DC |
| EC |
∴△ACD∽△BCE.
∴∠DAC=∠EBC=60°.
∴∠DAC=∠ACB.
∴AD∥BC.
成立.
(3)∵△ABC是等腰三角形、△DEC是等腰直角三角形,△ABC∽△DEC,
∴∠ACB=∠DCE.
∴
| AC |
| BC |
| DC |
| EC |
∴△ACD∽△BCE.
∴∠DAC=∠EBC.
∴∠DAC=∠ACB.
∴AD∥BC.
点评:观察测量,然后进行推理证明,是数学知识发现的基本规律.本题考查了等腰直角三角形,正三角形,等腰三角形的性质,相似三角形的判定和性质,平行线的判定.注意证明方式相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



