题目内容
化简或求值:(1)若1<x<2,化简
| |x-2| |
| x-2 |
| |x-1| |
| 1-x |
| |x| |
| x |
(2)已知a+b+c=0,求:a(
| 1 |
| b |
| 1 |
| c |
| 1 |
| c |
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
(3)若解关于x的分式方程
| 2 |
| x-2 |
| mx |
| x2-4 |
| 3 |
| x+2 |
分析:(1)在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号;
(2)把所求的代数式展开整理成条件中有关的形式把a=-b-c、b=-a-c、c=-a-b代入即可;
(3)分式方程的增根是令分母等于0的x值.
(2)把所求的代数式展开整理成条件中有关的形式把a=-b-c、b=-a-c、c=-a-b代入即可;
(3)分式方程的增根是令分母等于0的x值.
解答:解:(1)∵1<x<2,
∴原式=-1+1+1=1;
(2)原式=
+
+
+
+
+
=
+
+
;
因为a+b+c=0,
所以a=-b-c,b=-a-c,c=-a-b;
代入,得:原式=-3.
(3)去分母得,(m-1)x=-10;
∵分式方程有增根,所以增根是x=±2;
∴m=-4或6.
∴原式=-1+1+1=1;
(2)原式=
| a |
| b |
| a |
| c |
| b |
| c |
| b |
| a |
| c |
| a |
| a |
| b |
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
因为a+b+c=0,
所以a=-b-c,b=-a-c,c=-a-b;
代入,得:原式=-3.
(3)去分母得,(m-1)x=-10;
∵分式方程有增根,所以增根是x=±2;
∴m=-4或6.
点评:主要考查了绝对值,代数式的化简求值和分式方程的增根问题.解此题的关键是在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号;把所求的代数式展开整理成条件中有关的形式把a=-b-c;b=-a-c;c=-a-b代入即可.分式方程的增根是令分母等于0的x值.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
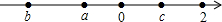 化简或求值:
化简或求值: 化简或求值
化简或求值 化简或求值:
化简或求值: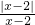 -
-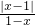 +
+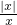 ;
;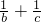 )+b(
)+b(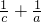 )+c(
)+c(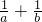 )的值.
)的值.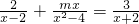 会产生增根,求m的值.
会产生增根,求m的值.