题目内容
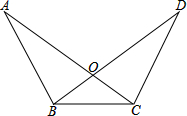 如图,∠DBC=∠ACB,∠ABD=∠DCA,若△ABC的周长为14,BC=4,则△COD的周长为( )
如图,∠DBC=∠ACB,∠ABD=∠DCA,若△ABC的周长为14,BC=4,则△COD的周长为( )分析:先可以由条件得出∠ABC=∠DCB,就可以得出△ABC≌△DCB,就可以得出AC=BD,AB=CD,进而由△ABC的周长为14求出结论.
解答:解:∵∠DBC=∠ACB,
∴OB=OC.
∵∠ABD=∠DCA,
∴∠DBC+∠ABD=∠DCA+∠ACB,
∴∠ABC=∠DCB.
在△ABC和△DCB中,
,
∴△ABC≌△DCB(ASA),
∴AB=CD,AC=DB.
∴AC-OC=DB-OB,
即AO=DO.
∵AB+BC+AC=AB+AO+OC+CB=14,
∴CD+DO+OC+CB=14.
∵BC=4,
∴CD+DO+0C=10,
即△COD的周长为10.
故选B.
∴OB=OC.

∵∠ABD=∠DCA,
∴∠DBC+∠ABD=∠DCA+∠ACB,
∴∠ABC=∠DCB.
在△ABC和△DCB中,
|
∴△ABC≌△DCB(ASA),
∴AB=CD,AC=DB.
∴AC-OC=DB-OB,
即AO=DO.
∵AB+BC+AC=AB+AO+OC+CB=14,
∴CD+DO+OC+CB=14.
∵BC=4,
∴CD+DO+0C=10,
即△COD的周长为10.
故选B.
点评:本题考查了等式的性质的运用,全等三角形的判定及性质的运用,三角形的周长的运用,解答时证明三角形全等是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
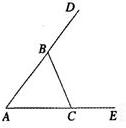
 如图,∠DBC=30°,AB=DB,利用此图求tan75°=
如图,∠DBC=30°,AB=DB,利用此图求tan75°=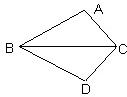 28、附加题:如图△ABC≌△DBC,∠A=110°,则∠D=
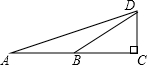
28、附加题:如图△ABC≌△DBC,∠A=110°,则∠D=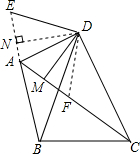 如图,△DBC中,DB=DC,A为△DBC外一点,且∠BAC=∠BDC,DM⊥AC于M,求
如图,△DBC中,DB=DC,A为△DBC外一点,且∠BAC=∠BDC,DM⊥AC于M,求