题目内容
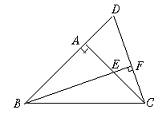
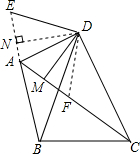如图，△DBC中，DB=DC，A为△DBC外一点，且∠BAC=∠BDC，DM⊥AC于M，求| AC-AB | AM |
分析：在AC上截取CF=AB，由∠BAC=∠BDC就可以得出∠FCD=∠ABD，在△DCF和△DBA中由SAS就可以得出△DCF≌△DBA，就有AD=FD，由DM⊥AC就可以得出AF=2AM而得出结论．
解答：解：在AC上截取CF=AB，连接DF
∵∠BAC=∠BDC，且∠DEC=∠AEB，
∴∠FCD=∠ABD．
在△DCF和△DBA中
，
∴△DCF≌△DBA（SAS），
∴DF=DA．
∵DM⊥AC，
∴AF=2AM．
∵AF=AC-FC，
∴AF=AC-AB，
∴AC-AB=2AM．
∴
=
=2．
答：
=2．
∵∠BAC=∠BDC，且∠DEC=∠AEB，
∴∠FCD=∠ABD．
在△DCF和△DBA中
|
∴△DCF≌△DBA（SAS），
∴DF=DA．
∵DM⊥AC，
∴AF=2AM．
∵AF=AC-FC，
∴AF=AC-AB，
∴AC-AB=2AM．
∴
| AC-AB |
| AM |
| 2AM |
| AM |
答：
| AC-AB |
| AM |
点评：本题考查截取法在作辅助线中的运用，三角形内角和定理的运用，三角形全等的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
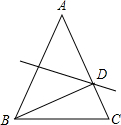如图，△ABC中AB=AC，AB的垂直平分线交AC于点D．若∠A=40°，则∠DBC=
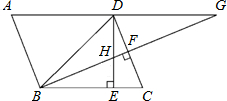已知：如图，?ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE、BF相交于点H，BF、AD的延长线相交于点G．
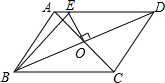如图，?ABCD中，AB=6，AD=8，AC、BD相交于点O，OE⊥BD交AD于点E，则∠EBD