题目内容
阅读并解答下列问题：我们熟悉两个乘法公式：①（a+b）2=a2+2ab+b2；②（a-b）2=a2-2ab+b2．现将这两个公式变形，可得到一个新的公式③：ab=（| a+b |
| 2 |
| a-b |
| 2 |
例如：因式分解：（ab-1）2+（a+b-2）（ a+b-2ab）
解：原式=（ab-1）2+[
| (a+b-2)-(a+b-2ab) |
| 2 |
| (a+b-2)-(a+b-2ab) |
| 2 |
=（ab-1）2+（a+b-ab-1）2-（ab-1）2=（a-1）（b-1）2=（a-1）2（b-1）2
你能利用公式（或其他方法）解决下列问题吗？
已知各实数a，b，c满足ab=c2+9且a=6-b，求证：a=b．
分析：先将ab=c2+9变形为（
）2-（
）2=c2+9，再将a+b=6代入可得-（
）2=c2，根据非负数的性质即可得证．
| a+b |
| 2 |
| a-b |
| 2 |
| a-b |
| 2 |
解答：解：已知a=6-b，则a+b=6，
（
）2-（
）2=c2+9，
（
）2-（
）2=c2+9，
9-（
）2=c2+9，
-（
）2=c2，
则（
）2=c2=0，
a-b=0，
∴a=b．
（
| a+b |
| 2 |
| a-b |
| 2 |
（
| a+b |
| 2 |
| a-b |
| 2 |
9-（
| a-b |
| 2 |
-（
| a-b |
| 2 |
则（
| a-b |
| 2 |
a-b=0，
∴a=b．
点评：本题考查了因式分解的应用，根据完全平方公式整理成-（
）2=c2的形式是求解的关键．
| a-b |
| 2 |
练习册系列答案
相关题目
+b）2=
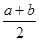)2-(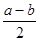
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
+
-
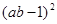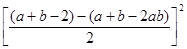+b）2=
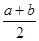)2-(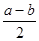
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
+
-
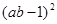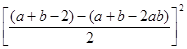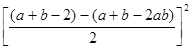
）2-（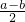
）2，这个公式形似平方差公式，我们不妨称之为广义的平立差公式．灵活、恰当地运用公式③将会使一些数学问题迎刃而解．
-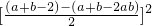