题目内容
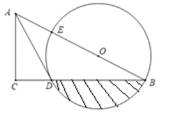
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限,
在第一象限,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() .
.
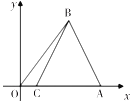
(1)求证:![]() ;
;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)cos∠ABO=![]()
【解析】
(1)过点![]() 作
作![]() 点
点![]() ,在
,在![]() 中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
(2)在![]() 中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
(1)在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,
,
![]() ,∠OAB=∠ABO,
,∠OAB=∠ABO,
过点![]() 作
作![]() 点
点![]() ,
,
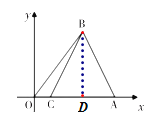
则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴CD=6-2=4,
∴BC=![]() ,
,
∴AB=BC,
∴∠ACB=∠BAO,
∴∠ACB=∠ABO=∠BAO,
又∵∠BAC=∠OAB,
![]() (两角分别相等的两个三角形相似);
(两角分别相等的两个三角形相似);
(2)在![]() 中,
中,
![]() ,
,
∵∠ABO=∠BAO ,
![]() ,
,
即![]() 的值为
的值为![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目