题目内容
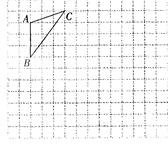
如图，方格纸上的每个小方格都是边长为1小正方形，我们把格点连线为边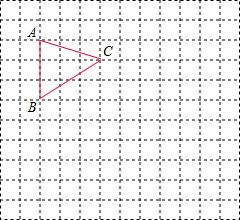
的三角形称为“格点三角形”，图中的△ABC就是一个格点三角形．（1）填空：AC=
（2）请先在方格纸中画出一个格点三角形DEF，使△DEF∽△ABC，并且DE：AB=3：1．再回答：△DEF与△ABC的周长之比为
分析：（1）根据勾股定理可以求出AC的长，在Rt△CMB中求出tanB的值．
（2）根据△DEF∽△ABC，并且DE：AB=3：1，先画出符合要求的格点三角形，然后再根据相似三角形的相似比等于周长比即可得出答案．
（2）根据△DEF∽△ABC，并且DE：AB=3：1，先画出符合要求的格点三角形，然后再根据相似三角形的相似比等于周长比即可得出答案．
解答：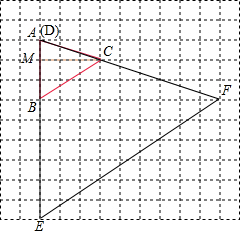
解：（1）根据AC2=32+12
∴BC=
，
tanB=
=
，
故答案为：AC=
，tanB=
；
（2）所画格点三角形DEF如下图所示，
∵△DEF∽△ABC，并且DE：AB=3：1．
∴△DEF与△ABC的周长之比为：3：1．
故答案为：3：1．
解：（1）根据AC2=32+12∴BC=
| 10 |
tanB=
| CM |
| BM |
| 3 |
| 2 |
故答案为：AC=
| 10 |
| 3 |
| 2 |
（2）所画格点三角形DEF如下图所示，
∵△DEF∽△ABC，并且DE：AB=3：1．
∴△DEF与△ABC的周长之比为：3：1．
故答案为：3：1．
点评：此题主要考查了相似图形的性质以及相似图形的画法，正确的画出符合要求的相似三角形是解决问题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
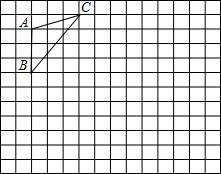如图，方格纸上的每个小方格都是边长为1的正方形，我们把格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是一个格点三角形．
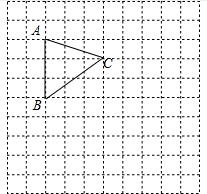如图，方格纸上的每个小方格都是边长为1小正方形，我们把格点连线为边的三角形称为“格点三角形”，图中的△ABC就是一个格点三角形．
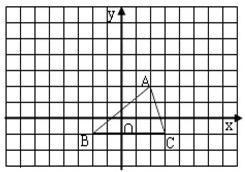21、如图，方格纸上的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形．在建立平面直角坐标系后，点B的坐标为（-2，-1）．