题目内容
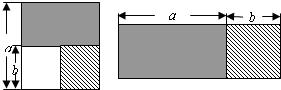
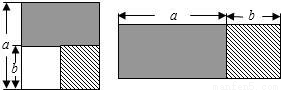
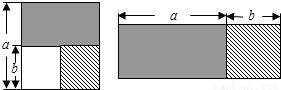
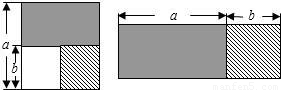
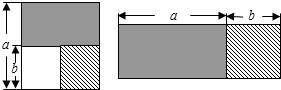
从边长为a的正方形中去掉一个边长为b的小正方形，如图，然后将剩余部分剪后拼成一个矩形，上述操作所能验证的等式是
- A.a2-b2=（a+b）（a-b）
- B.（a-b）2=a2-2ab+b2
- C.（a+b）2=a2+2ab+b2
- D.a2+ab=a（a+b）
A
分析：由大正方形的面积-小正方形的面积=矩形的面积，进而可以证明平方差公式．
解答：大正方形的面积-小正方形的面积=a2-b2，
矩形的面积=（a+b）（a-b），
故a2-b2=（a+b）（a-b）．
故选A．
点评：本题主要考查平方差公式的几何意义，用两种方法表示阴影部分的面积是解题的关键．
分析：由大正方形的面积-小正方形的面积=矩形的面积，进而可以证明平方差公式．
解答：大正方形的面积-小正方形的面积=a2-b2，
矩形的面积=（a+b）（a-b），
故a2-b2=（a+b）（a-b）．
故选A．
点评：本题主要考查平方差公式的几何意义，用两种方法表示阴影部分的面积是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
