Question

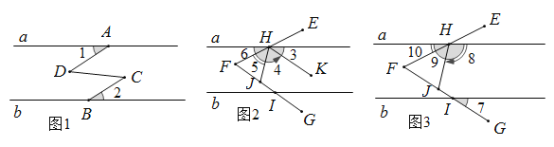
【题目】如图①：MA1∥NA2，图②：MA1∥NA3，图③：MA1∥NA4，图④：MA1∥NA5，……，

则第8个图中的∠A1+∠A2+∠A3+…+∠A8＝_____．

Answer 1

【答案】1260°．

【解析】

分别求出图①、图②、图③中，这些角的和，探究规律后，利用规律解题即可．

解：∵MA1与NAn平行，

∴在图①可得∠A1+∠A2＝180°，

在②中可过A2作A2B∥MA1，如图．

∵MA1∥NA3，

∴A2B∥NA3，

∴∠MA1A2+∠BA2A1＝∠BA2A3+∠NA3A2＝180°，

∴∠A1+∠A2+∠A3＝360°，

同理可得∠A1+∠A2+∠A3+∠A4＝540°，

∵∠A1+∠A2＝180°＝1×180°，

∠A1+∠A2+∠A3＝360°＝2×180°，

∠A1+∠A2+∠A3+∠A4＝540°＝3×180°，

∴∠A1+∠A2+∠A3++…+∠A8＝7×180°＝1260°．

故答案为：1260°．