题目内容
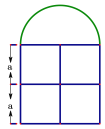
【题目】如图是由边长相同的小正方形组成的网格,A、B、P、Q四点均在正方形网格的格点上,线段AB、PQ相交于点M,则线段AM的长为_____.

【答案】![]()
【解析】分析:连接AP、PB、AQ,利用勾股定理逆定理证∠PAB=∠ABQ=90°,结合∠AMP=∠BMQ证△APM∽△BQM,得![]() =3,即可知
=3,即可知![]() =
=![]() ,据此可得答案.
,据此可得答案.
详解:如图,连接AP、PB、AQ,
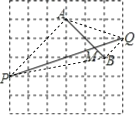
∵AP2=18、AB2=8、PB2=26,
∴AP2+AB2=PB2,
∴△PAB为直角三角形,∠PAB=90°,
∵AQ2=10、AB2=8、BQ2=2,
∴AB2+BQ2=AQ2,
∴△ABQ为直角三角形,∠ABQ=90°,
∵∠AMP=∠BMQ,
∴△APM∽△BQM,
∴![]() =
=![]() =3,
=3,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AM=![]() ,
,
故答案为: ![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目