题目内容
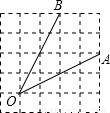
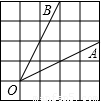
如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .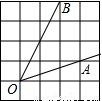
【答案】分析:首先连接AB,由勾股定理易求得OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,然后由勾股定理的逆定理,可证得△AOB是等腰直角三角形,继而可求得cos∠AOB的值.
解答: 解:连接AB,
解:连接AB,
∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°= .
.
故答案为: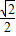 .
.
点评:此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
解答:
 解:连接AB,
解:连接AB,∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°=
 .
.故答案为:
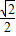 .
.点评:此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
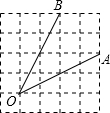 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是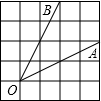 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是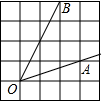 (2012•仪征市一模)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
(2012•仪征市一模)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是