题目内容
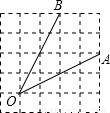
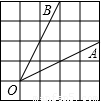
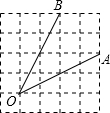 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是分析:先结合图,根据勾股定理易求OA、OB、AB,从而可知△AOB是等腰三角形,进而可求其AB上的高,利用三角形的面积公式易求OA上的高,再利用勾股定理可求BE,利用余弦定义可求cos∠AOB.
解答: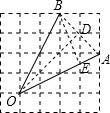 解:过B作BE⊥OA于E,过O作OD⊥AB于D,设每一格的边长是1,则
解:过B作BE⊥OA于E,过O作OD⊥AB于D,设每一格的边长是1,则
OB=
=2
,
同理OA=
=2
,
AB=
=2
,
∴OA=OB,
∵OD⊥AB,
∴AD=BD=
,
∴OD=
=3
,
∵S△AOB=
AB•OD=
OA•BE
∴2
×3
=2
•BE,
∴BE=
,
在Rt△OBE中,OE=
=
,
∴cos∠AOB=
=
.
故答案是
.
 解:过B作BE⊥OA于E,过O作OD⊥AB于D,设每一格的边长是1,则
解:过B作BE⊥OA于E,过O作OD⊥AB于D,设每一格的边长是1,则OB=
| 22+42 |
| 5 |
同理OA=
| 42+22 |
| 5 |
AB=
| 22+22 |
| 2 |
∴OA=OB,
∵OD⊥AB,
∴AD=BD=
| 2 |
∴OD=
| 20-2 |
| 2 |
∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴2
| 2 |
| 2 |
| 5 |
∴BE=
| 6 | ||
|
在Rt△OBE中,OE=
20-
|
| 8 | ||
|
∴cos∠AOB=
| OE |
| OB |
| 4 |
| 5 |
故答案是
| 4 |
| 5 |
点评:本题考查了勾股定理、锐角三角函数的计算,解题的关键作辅助线,构造直角三角形.

练习册系列答案
相关题目
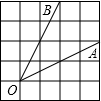 如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是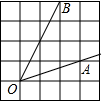 (2012•仪征市一模)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是
(2012•仪征市一模)如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是