题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点,与y轴交于点C,BO=CO.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.

【答案】(1)y=﹣x2+2x+3.(2)S =![]() t2.(3)m=
t2.(3)m=![]() .
.
【解析】试题分析:(1)由ax2﹣2ax﹣3a=0时,解得x=3或﹣1,推出A(﹣1,0),B(3,0),推出OA=1,OB=3,推出OC=OB=3,推出﹣3a=3,可得a=﹣1,即可解决问题;
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.P(t,﹣t2+2t+3,由∠PAE=∠DAO,可得tan∠PAE=tan∠DAO,可得![]() ,即
,即![]() ,可得OD=3﹣t,CD=3﹣OD=t,再根据S=
,可得OD=3﹣t,CD=3﹣OD=t,再根据S=![]() PKCD=计算即可;
PKCD=计算即可;
(3)首先证明△PKM≌△PKN,推出PM=PN,MK=NK,再证明△HON≌△PKN,推出PK=HO,由∠3=∠5,可得tan∠3=tan∠5,可得![]() ,BE=OB﹣OE=3﹣t,即
,BE=OB﹣OE=3﹣t,即![]() ,可得GE=1,推出OH=2EG=2,推出PK=2,PE=3,推出OK=3=OC,推出点K与点C重合,由此即可解决问题.
,可得GE=1,推出OH=2EG=2,推出PK=2,PE=3,推出OK=3=OC,推出点K与点C重合,由此即可解决问题.
试题解析:(1)当ax2﹣2ax﹣3a=0时,解得x=3或﹣1,
∴A(﹣1,0),B(3,0),∴OA=1,OB=3,∴OC=OB=3,∴﹣3a=3,∴a=﹣1,
∴y=﹣x2+2x+3.
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.
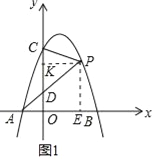
∵点P在第一象限,横坐标为t,∴P(t,﹣t2+2t+3),
∵∠PKO=∠COB=∠PEO=90°,∴四边形KPEO是矩形,∴PK=OE=t,PE=OK,
∴PE=﹣t2+2t+3,AE=t+1,
∵∠PAE=∠DAO,∴tan∠PAE=tan∠DAO,∴![]() ,∴
,∴![]() ,
,
∴OD=3﹣t,∴CD=3﹣OD=t,
∴S=![]() PKCD=
PKCD=![]() t2.
t2.
(3)设PH交y轴于点N.
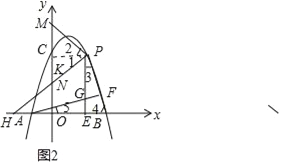
∵∠PKO=∠PKM=∠HON=90°,∴PK∥x轴,∴∠1=∠PHB,
∵∠MPH=2∠PHB,∴MPH=2∠1,即∠1=∠2,
∵∠PKM=∠PKN,PK=PK,∴△PKM≌△PKN,∴PM=PN,MK=NK,
∵PH=2PM,∴PN=HN,
∵∠HON=∠PKN,∠1=∠BHP,∴△HON≌△PKN,∴PK=HO,KN=ON,
∵AF⊥PB,∴∠AFB=90°,∴∠3+∠4=90°,
∵∠PEB=90°,∴∠4+∠5=90°,∴∠3=∠5,∴tan∠3=tan∠5,
∴![]() ,∵BE=OB﹣OE=3﹣t,∴
,∵BE=OB﹣OE=3﹣t,∴![]() ,∴GE=1,
,∴GE=1,
∴OH=2EG=2,∴PK=2,PE=3,∴OK=3=OC,∴点K与点C重合,∴KN=![]() ,
,
∴OM=3KN=![]() ,即m=
,即m=![]() .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案