��Ŀ����
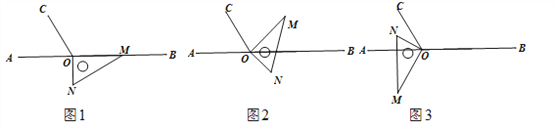
����Ŀ����ͼ1����OΪֱ��AB��һ��������O������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB������һ��ON��ֱ��AB���·���
��1����ͼ2����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ʹ��OM����BOC���ڲ�����OMǡ��ƽ����BOC����ʱ��AOM=_______����
��2����ͼ3��������ͼ2�е����ǰ��Ƶ�O����ʱ�뷽����ת��ʹ��ON����AOC���ڲ���̽����AOM����NOC֮��������ϵ����˵�����������
��3����ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ�����ʱ�뷽����תһ��������ת�Ĺ���������ֱ��ONǡ��ƽ����AOC�����ʱ���ǰ��Ƶ�O��ת��ʱ���Ƕ����룿��ֱ��д���𰸼���������˵��������
���𰸡���1��120����2����AOM����NOC =30������3��6���24��
�������������������1������OMǡ��ƽ�֡�BOC���á�BOC�Ķ�������2�������BOM�Ķ��������������AOM�Ķ����Ƕ��٣�
��2�����ȸ��ݡ�AOM-��NOC=30������BOC=120���������A0C=60����Ȼ����ݡ�AON=90��-��AOM=60��-��NOC���жϳ���AOM���NOC֮������ʲô������ϵ���ɣ�
��3�����������ǰ��Ƶ�O��ת��ʱ����x�룬���ݡ�BOC=120�����ɵá�AOC=60������BON=��COD=30����Ȼ�������ת60��ʱONƽ�֡�AOC���ɵ�10x=60��10x=240���ݴ����x��ֵ�Ƕ��ټ��ɣ�
�����������1����OMǡ��ƽ�֡�BOC��
���BOM=120���2=60����
���AOM=180��-60��=120����
��2����ͼ3��
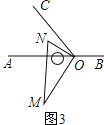 ��
��
��AOM-��NOC=30����
�ߡ�BOC=120����
���A0C=60����
�ߡ�AON=90��-��AOM=60��-��NOC��
���AOM-��NOC=30����
��3�������ǰ��Ƶ�O��ת��ʱ����x�룬
�ߡ�BOC=120����
���AOC=60����
���BON=30����
����ת60��ʱONƽ�֡�AOC��
��10x=60��10x=240��
��x=6��x=24��
����ʱ���ǰ��Ƶ�O��ת��ʱ����6��24�룮

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�