题目内容
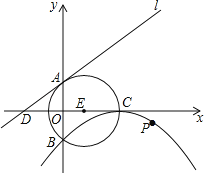
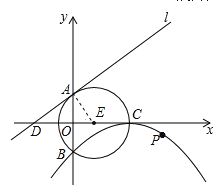
【题目】如图，⊙E的圆心E(3，0)，半径为5，⊙E与y轴相交于A、B两点(点A在点B的上方)，与x轴的正半轴相交于点C；直线l的解析式为y=
x＋4，与x轴相交于点D；以C为顶点的抛物线经过点B.
(1)求抛物线的解析式；
(2)判断直线l与⊙E的位置关系，并说明理由；
(3) 动点P在抛物线上，当点P到直线l的距离最小时，求出点P的坐标及最小距离.
【答案】（1）y=-
x2+x-4；（2）直线l与⊙E相切与A．(3) 抛物线上的动点P的坐标为（2，-
）时，点P到直线l的距离最小，其最小距离为
．
【解析】
试题分析：（1）连接AE，由已知得：AE=CE=5，OE=3，利用勾股定理求出OA的长，结合垂径定理求出OC的长，从而得到C点坐标，进而得到抛物线的解析式；
（2）求出点D的坐标为（-
，0），根据△AOE∽△DOA，求出∠DAE=90°，判断出直线l与⊙E相切与A．
（3）过点P作直线l的垂线段PQ，垂足为Q，过点P作直线PM垂直于x轴，交直线l于点M．设M（m，
m+4），P（m，-m2+m-4），得到PM=m+4-（-m2+m-4）=m2-
m+8=（m-2）2+
，根据△PQM的三个内角固定不变，得到PQ最小=PM最小
sin∠QMP=PM最小sin∠AEO=×
=
，从而得到最小距离．
试题解析：（1）如图1，连接AE，由已知得：AE=CE=5，OE=3，
在Rt△AOE中，由勾股定理得，OA=
，
∵OC⊥AB，
∴由垂径定理得，OB=OA=4，
OC=OE+CE=3+5=8，
∴A（0，4），B（0，-4），C（8，0），
∵抛物线的顶点为C，
∴设抛物线的解析式为y=a（x-8）2，
将点B的坐标代入上解析的式，得64a=-4，故a=-，
∴y=-（x-8）2，
∴y=-x2+x-4为所求抛物线的解析式，
（2）在直线l的解析式y=x+4中，令y=0，得x+4=0，解得x=-
，
∴点D的坐标为（-，0），
当x=0时，y=4，
∴点A在直线l上，
在Rt△AOE和Rt△DOA中，
∵
，
，
∴
，
∵∠AOE=∠DOA=90°，
∴△AOE∽△DOA，
∴∠AEO=∠DAO，
∵∠AEO+∠EAO=90°，
∴∠DAO+∠EAO=90°，即∠DAE=90°，因此，直线l与⊙E相切与A．
（3）如图2，过点P作直线l的垂线段PQ，垂足为Q，过点P作直线PM垂直于x轴，交直线l于点M．
设M（m，
m+4），P（m，-m2+m-4），则
PM=m+4-（-m2+m-4）=m2-
m+8=（m-2）2+
，
当m=2时，PM取得最小值，
此时，P（2，-
），
对于△PQM，
∵PM⊥x轴，
∴∠QMP=∠DAO=∠AEO，
又∠PQM=90°，
∴△PQM的三个内角固定不变，
∴在动点P运动的过程中，△PQM的三边的比例关系不变，
∴当PM取得最小值时，PQ也取得最小值，
PQ最小=PM最小sin∠QMP=PM最小sin∠AEO=×
=，
∴当抛物线上的动点P的坐标为（2，-）时，点P到直线l的距离最小，其最小距离为．
