题目内容
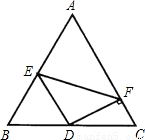
 已知如图,D是边长为4的正△ABC的边BC上一点,ED∥AC交AB于E,DF⊥AC交AC于F,设DF=x.
已知如图,D是边长为4的正△ABC的边BC上一点,ED∥AC交AB于E,DF⊥AC交AC于F,设DF=x.(1)求△EDF的面积y与x的函数关系式和自变量x的取值范围.
(2)当x为何值时,△EDF的面积最大,最大面积是多少?
(3)若△DCF与由E、F、D三点组成的三角形相似,求BD的长.
分析:(1)判断出△BDE和△DEF的形状,利用60°的正弦值用DF表示出DC,进而得到BD,DE,利用三角形的面积公式求得函数关系式.
(2)由相似得到△DEF是含30°的直角三角形,可利用所给的2个特殊的直角三角形都用BD表示出DF的长度,然后即可求得BD长.
(2)由相似得到△DEF是含30°的直角三角形,可利用所给的2个特殊的直角三角形都用BD表示出DF的长度,然后即可求得BD长.
解答:解:(1)∵△ABC是正三角形,且ED∥AC,
∴△BDE∽△BCA,
∴△BDE是等边三角形,∠FDC=30°,
∴CD=DF÷sin60°=
x.
∠EDF=90°,
BD=BC-CD=ED=4-
x.
y=DF×ED÷2=
x(4-
x)=-
x2+2x,
∵D在BC上,
∴CD<4,
当CD=4时,CF=2,DF=2
,
DF≤2
(等于2
时,D和B重合)
∴自变量x的取值范围0≤x≤2
.
(2)∵y=-
x2+2x,
=-
(x-
)2+
,
∴当x=
,△EDF的面积最大.
最大面积是=
.
(3)当△DCF∽△EFD,
∴∠FED=∠FDC=30°.
∴DF=
DE=
BD.
∵DC=4-BD,∠C=60°,
∴DF=
CD=
,
∴
BD=
.
解得:BD=2.4.
当△DCF∽△FED,
同理可得:BD=
,
∴BD=
或2.4.
∴△BDE∽△BCA,
∴△BDE是等边三角形,∠FDC=30°,
∴CD=DF÷sin60°=
2
| ||
| 3 |
∠EDF=90°,
BD=BC-CD=ED=4-
2
| ||
| 3 |
y=DF×ED÷2=
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
∵D在BC上,
∴CD<4,
当CD=4时,CF=2,DF=2
| 3 |
DF≤2
| 3 |
| 3 |
∴自变量x的取值范围0≤x≤2
| 3 |
(2)∵y=-
| ||
| 3 |
=-
| ||
| 3 |
| 3 |
| 3 |
∴当x=
| 3 |
最大面积是=
| 3 |
(3)当△DCF∽△EFD,
∴∠FED=∠FDC=30°.
∴DF=
| ||
| 3 |
| ||
| 3 |
∵DC=4-BD,∠C=60°,

∴DF=
| ||
| 2 |
4
| ||||
| 2 |
∴
| ||
| 3 |
4
| ||||
| 2 |
解得:BD=2.4.
当△DCF∽△FED,
同理可得:BD=
| 4 |
| 3 |
∴BD=
| 4 |
| 3 |
点评:考查特殊三角形的判断以及特殊三角函数值的充分运用.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
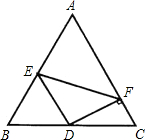 已知如图,D是边长为4的正△ABC的边BC上一点,ED∥AC交AB于E,DF⊥AC交AC于F,设DF=x.
已知如图,D是边长为4的正△ABC的边BC上一点,ED∥AC交AB于E,DF⊥AC交AC于F,设DF=x.